Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 83

Um pequeno disco com diâmetro D1 = 50 mm e emissividade ε1 = 0,6 é mantido a uma temperatura de T1 = 900 K. O disco é coberto com uma barreira de radiação hemisférica com o mesmo diâmetro e uma emissividade ε2 = 0,02 (ambos os lados). O disco e a redoma estão

localizados na base de um grande recipiente refratário (ε4 = 0,85), onde há vácuo, defronte a outro disco com diâmetro D3 = D1, emissividade ε3 = 0,4 e temperatura T3 = 400 K. O fator de forma F23 da barreira em relação ao disco superior é igual a 0,3.

  1. Construa um circuito térmico equivalente ao sistema em análise. Identifique todos os nós, resistências e correntes.
  2. Determine a taxa de transferência de calor líquida entre o disco quente e o resto do sistema.

Passo 1

Vamos lá!! Pra começar com o pé direito a gente vai pegar tudo o que o problema ta falando pra a gente e transformar em um esqueminha, pra visualizarmos melhor o que ta acontecendo!!

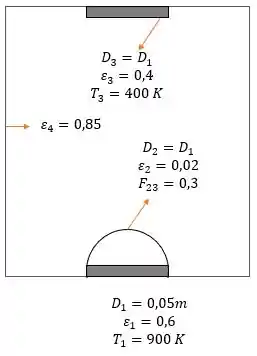
Desenhando a resistência:

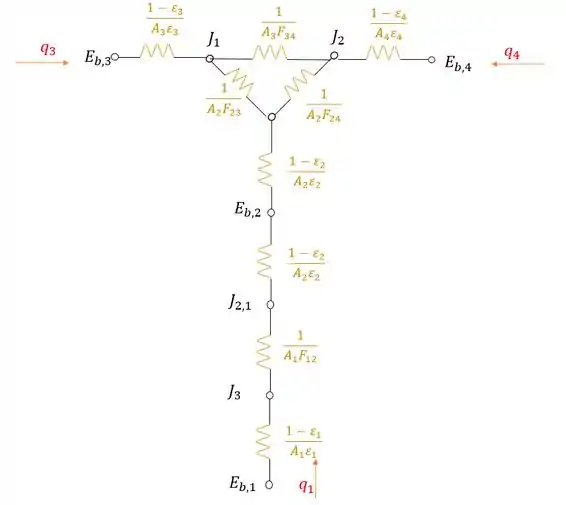
Passo 2

Para determinar a transferência de calor líquida entre o disco quente (superfície 1 ) com o resto do ambiente, q 1 , para isso usamos a seguinte expressão:

q 1 = σ ( T 1 4 - T 3 4 ) 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 2 1 - ε 2 ε 2 A 2 1 A 2 F 23 + 1 A 2 F 24 + 1 A 3 F 34 - 1 + 1 - ε 3 ε 3 A 3

Precisamos conhecer os fatores de forma!!

A superfície 1 é completamente envolta da superfície 2 , logo F 12 = 1 !

Pela regra da soma F 23 + F 24 = 1 então F 24 = 1 - 0,3 = 0,7 !

Pela regra da soma:

F 34 = 1 - F 32

Agora pela regra da reciprocidade:

A 3 F 32 = A 2 F 23

Substituindo:

F 34 = 1 - A 2 A 3 F 23

Calculando:

F 34 = 1 - π D 2 2 π D 2 4 F 23 = 1 - 2 × 0,3 = 0,4

Agora vamos calcular as áreas!!

A 1 = A 3 = π D 2 4 = π 0,05 2 4 = 1,963 × 10 - 3   m 2

A 2 = π D 2 2 = 2 A 1

Nesse caso, podemos isolar A 1 :

q 1 = σ ( T 1 4 - T 3 4 ) A 1 1 - ε 1 ε 1 + 1 F 12 + 2 1 - ε 2 2 ε 2 1 2 F 23 + 1 2 F 24 + 1 F 34 - 1 + 1 - ε 3 ε 3

Passo 3

Com todos os dados, podemos substituir!!!

q 1 = 5,67 × 10 - 8 ( 900 4 - 400 4 ) 1,963 × 10 - 3   1 - 0,6 0,6 + 1 1 + 2 1 - 0,02 2 × 0,02 1 2 × 0,3 + 1 2 × 0,7 + 1 0,4 - 1 + 1 - 0,4 0,4

Calculando:

q 1 = 1,32   W

Aweeee!!!

Resposta

q 1 = 1,32   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

103 - Considere dois discos paralelos coaxiais de diâmetros a e b , mostrado na Fig. P13-103.Para essa geometria, o fator de forma do disco menor para o disco maior pode ser calculado por F = 0,5 B A
112 - Um coletor solar é constituído por um tubo de cobre horizontal de 5c m de diâmetro externo envolto por um tubo de vidro fino concêntrico de 12c m de diâmetro.A água é aquecida à medida que flui
104 - Um grande número de longos tubos, cada um com diâmetro D , é colocado paralelo um ao outro e com distância centro a centro s .Uma vez que todos os tubos são geometricamente semelhantes e estão n
113 - Dois discos paralelos concêntricos, 20c m e 40c m de diâmetro são separados por uma distância de 10c m .O disco menor ( ε = 0,80 ) se encontra a uma temperatura de 300° C .O disco maior ε = 0,60
Considere um forno hemisférico com uma base circular plana de diâmetro D. Determine o fator de forma da cúpula desse forno até sua base.