As perdas na válvula borboleta da figura 6.19b podem ser associadas a um tipo de dispositivo de obstrução de Bernoulli, como na figura 6.39. A área da garganta, Ag na equação 6.104 pode ser interpretada como sendo a área das duas aberturas ao redor do disco borboleta quando vistas a montante. Primeiramente, ajuste a perda média em função do ângulo de abertura na figura 6.19b a uma curva exponencial. Em seguida, use sua curva ajustada para calcular o “coeficiente de descarga” de uma válvula borboleta em função do ângulo de abertura. Plote os resultados e compare com aqueles para um medidor de vazão típico.
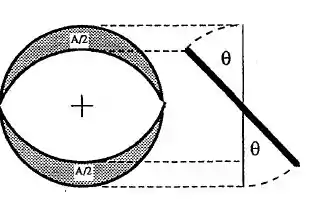
Passo 1
E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?
As duas aberturas que são referidos são mostradas na imagem acima. A área total das aberturas são iguais a área total reduzida por um fatorzinho, se liga!!
Onde e é o raio da válvula e tubo.
Passo 2
A velocidade efetiva passante através das aberturas pode ser calculada pela nossa velha e saudosa continuidade!!
Se as perdas foram realmente baseadas na velocidade efetiva, a gente pode calcular o seguinte:
Passo 3
Então a gente vai lá e pega o valor de tradicionalmente, ou seja, pela figura 6.19b do livro, multiplica ele por e “replota” um gráfico de por .
Vamos fazer isso para os três fabricantes que são mostrados na figura 6.19:
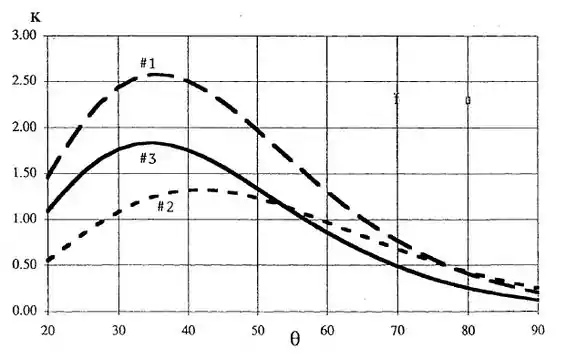
Note que todos os K’s estão agora em ordem de unidades, isso é bem melhor para correlacionar do que aqueles que são mostrados tipicamente na figura 6.19b
Resposta
Ei, a resposta está no passo a passo :)