Para permitir o cozimento de uma ampla gama de alimentos em fornos de micro-ondas, materiais de empacotamento metálicos e finos, que absorvem facilmente a energia das micro-ondas, foram desenvolvidos. Na medida em que o material de empacotamento é aquecido pelas micro-ondas, condução ocorre simultaneamente do empacotamento aquecido para o alimento frio. Seja o pedaço de carne esférico e congelado do Problema 5.33, que agora está embrulhado em um material de empacotamento fino que absorve micro-ondas. Determine o tempo necessário para a carne, que está bem próxima do material de empacotamento, atingir , quando da potência do forno ( total) são absorvidos no material de empacotamento.
Passo 1
Aqui nós temos a massa e temperaturas iniciais da carne congelada. Além também, da taxa de potência do microondas absorvida no material de embalagem. Ilustrando isso:
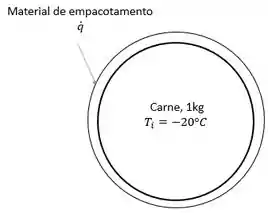
A partir disso, queremos encontrar o tempo para que a carne junto à embalagem atinja uma temperatura de .
Passo 2
Para resolver essa questão, vamos assumir que:
(1) A carne possui propriedades de gelo, que vão ser retiradas da Tabela A.3;
(2) A radiação e a convecção ao meio ambiente são desprezíveis;
(3) As propriedades são constantes;
(4) O material de embalagem possui uma capacidade de calor desprezível.
Desprezando as perdas de radiação e convecção, toda a energia absorvida no material de embalagem é conduzida para a carne e o fluxo de calor da superfície é:
O raio da esfera pode ser encontrado a partir da massa e da densidade:
Então,
Passo 3
Para um fluxo de calor constante na superfície, pode ser usada a relação na Tabela 5.2b (Casos interiores, esfera). Começamos calculando para .
Assumindo que temos:
E,
Como isso é menor que 0,2, nossa suposição estava correta. Finalmente, podemos resolver para o tempo: