Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 99

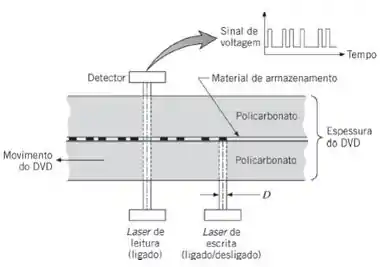
Um disco ótico regravável (DVD) é formado colocando-se um material de armazenamento composto binário, com 15   n m de espessura, entre duas folhas de 1   m m de policarbonato. Os dados são escritos no meio de armazenamento opaco pela sua irradiação, vinda de baixo, por um feixe de laser, relativamente de alta potência, com diâmetro 0,4   μ m e potência de 1   m W , o que resulta no rápido aquecimento do material composto (o policarbonato é transparente à irradiação do laser). Se a temperatura do meio de armazenamento exceder 900   K , um material amorfo não cristalino se forma no ponto aquecido quando a irradiação do laser é interrompida e permitido o rápido resfriamento do ponto. Os pontos resultantes de material amorfo têm uma diferente refletividade em relação ao material cristalino ao redor, de tal forma que eles podem ser lidos posteriormente com a irradiação com um segundo laser de menor potência e pela detecção das mudanças na radiação do laser transmitida através da espessura completa do DVD. Determine o tempo de irradiação (escrita) necessário para elevar a temperatura do meio de armazenamento de um valor inicial de 300   K para 1000   K . A absortividade do meio de armazenamento é de 0,8 . As propriedades do policarbonato são ρ   =   1200   k g / m 3 ,   k   =   0,21   W / ( m   ·   K ) e c p   =   1260   J / ( k g   ·   K ) .

Passo 1

Bora para mais uma questãozitcha! Aqui nós temos a espessura e propriedades do disco de DVD. Assim como o tamanho e a potência do ponto do laser.

A partir dessas informações queremos encontrar o tempo necessário para elevar o material de armazenamento de 300   K para 1000   K .

Passo 2

Para resolver essa questão vamos assumir que:

(1) As resistências de contato são desprezíveis nas interfaces;

(2) O meio é infinito;

(3) O policarbonato é transparente à radiação do laser;

(4) O policarbonato é opaco à radiação do ponto aquecido;

(5) A potência do laser é espacialmente uniforme;

(6) ) O movimento do disco não afeta a resposta térmica;

(7) O material de armazenamento é infinitamente fino;

(8) Os efeitos de transferência de calor em nanoescala são desprezíveis.

Ufa! Agora sim podemos resolver nossa questão em paz \o/

O calor transferido do material irradiado para armazenamento é:

q = α r P

Onde,

A s = π D 2 / 2

Passo 3

Da Tabela 5.2b para F o < 0,2 temos:

q * F o = q s ' ' L C k ( T s - T i ) = 1 2 π F o   + π 4  

E para F o ≥ 0,2 :

q * F o = q s ' ' L C k ( T s - T i ) = 0,77 F o + 2 2 π

Onde,

L c = A s 4 π 1 2 = D 8

q s ' ' = q A s

E,

F o = α t L c 2 = 8 α t D 2

Com,

α = k ρ c = 0,21 W m . K ( 1200 k g m 3 × 1260 J k g . K ) = 1,39 × 10 - 9   m 2 / s

Passo 4

A partir das expressões do passo anterior chegamos em:

q s ' ' L C k T s - T i = 2 P α r π D 8   k T S - T i                                            

                                                                                                                              = 2 × 1 × 10 - 3   W × 0,8 π × 0,4 × 10 - 6 × 8 × 0,21 W m . K × 1000 - 300 K

= 3,0623                                        

Com a primeira parcela da equação anterior é possível encontrar o valor de F o . Onde substituindo os valores nas duas primeiras equações do Passo 3 chegamos em:

F o = 0,151   para F o < 0,2

F o = 0,1 27   para F o ≥ 0,2

Sendo assim, comprovamos que F o < 0,2 . Ou seja, F o = 0,151 .

Da equação de F o , isolando o t encontramos:

t = F o D 2 8 α = 0,151 × 0,4 × 10 - 6 m 2 8 × 139 × 10 - 9 m 2 / s = 21,8 × 10 - 9   s

t = 21,8   n s

Resposta

t = 21,8   n s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma placa de espessura de 2,5 cm, um cilindro longo de diâmetro 2,5 cm e uma esfera de diâmetro 2,5 cm, todos inicialmente a 200 °C e todos feitos de bronze ( k=26W / m . ° Ceα=8,6 x 10 - 6
Grandes placas de um produto alimentar com 8 cm de espessura hermeticamente embaladas em papel fino são resfriados em uma câmara frigorífica mantida a 0 °C. O coeficiente de transferência de calor nas
Considere um bloco de motor de carro ( k=52W / m . Keα=1,7 x 10 - 5 m ² / s ² ). O motor pode ser considerado um bloco retangular cujos lados são 80, 40 e 40 cm. O motor está na temperatura de 150 °C
Um homem é encontrado morto em um quarto a 12°C. A temperatura da superfície sobre sua cintura é de 23°C, e o coeficiente de transferência de calor é estimado em 9 W m 2 K . Tratando o corpo como um c
86 – Durante os meses de inverno frio, um escritório é parcialmente aquecido extraindo energia térmica armazenado no solo abaixo, usando uma bomba de calor. Durante o verão, o prédio é parcialmente re