Revestimentos especiais são frequentemente formados pela deposição de finas camadas de um material fundido sobre um substrato sólido. A solidificação tem início na superfície do substrato e prossegue até que a espessura da camada solidificada se torne igual à espessura do depósito.

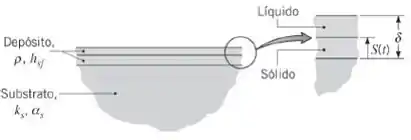
(a) Considere condições nas quais material fundido, à sua temperatura de fusão , é depositado sobre um grande substrato que se encontra inicialmente a uma temperatura uniforme . Com em , desenvolva uma expressão para estimar o tempo necessário para solidificar completamente o depósito, considerando que ele permanece à temperatura durante todo o processo de solidificação. Expresse o seu resultado em termos da condutividade térmica e da difusividade térmica do substrato da massa específica e do calor latente de fusão do depósito da espessura do depósito e das temperaturas relevantes .

(b) O processo de deposição por pulverização de plasma descrito no Problema 5.25 é usado para aplicar um fino revestimento de alumina sobre um espesso substrato de tungstênio. O substrato apresenta uma temperatura inicial uniforme , e as suas condutividade térmica e difusividade térmica podem ser aproximadas por e , respectivamente. A massa específica e o calor latente de fusão da alumina são e , respectivamente, e a alumina se solidifica na sua temperatura de fusão Supondo que a camada fundida seja depositada instantaneamente sobre o substrato, estime o tempo necessário para o depósito se solidificar.

Para resolver, vamos assumir que:

(1) O substrato pode ser aproximado como um meio semi-infinito no qual há condução dimensional;

(2) As camadas de alumina sólida e líquida permanecem à temperatura de fusão durante a solidificação (resistência insignificante à transferência de calor por condução através de sólido);

(3) A resistência de contato na interface revestimento / substrato é desprezível;

(4) A contração da solidificação é desprezível;

(5) As propriedades são constantes.

Na letra (a) queremos a expressão do tempo necessário para solidificar completamente o líquido. Ao realizar um balanço de energia na camada sólida, cuja espessura aumenta com , o calor latente liberado na interface sólido / líquido deve ser balanceado pela taxa de condução de calor no sólido. Então, por unidade de superfície, temos que:

Onde,

A partir das expressões acima, temos que:

Integrando em ,

Isolando o t:

Para a letra (b) queremos o tempo necessário para solidificar um revestimento de alumina. Então vamos substituir os valores na expressão encontrada na letra (a).