Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 187

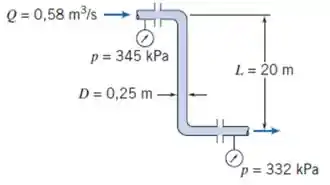
Petróleo bruto S G = 0,95 , proveniente de um petroleiro ancorado, escoa através de uma tubulação de 0,25   m de diâmetro com a configuração mostrada. A vazão é 0,58   m 3 / s e as pressões manométricas são mostradas no diagrama. Determine a força e o torque que são exercidos pela tubulação sobre os seus suportes.

Passo 1

Equações:

F = F S + F B = ∂ ∂ t ∫ V C V ρ d ∀ + ∫ S C V ρ V d A

r × F s + ∫ V C r × g ρ d ∀ + T e i x o = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Uniforme;
  3. Escoamento Estacionário;
  4. T e i x o = 0 ;
  5. Não há componente z de r × g ;
  6. F B x = 0 , g age na direção z .

Passo 2

Das equações apresentadas no Passo1, fazendo as considerações, temos:

F S x = ∫ S C u ρ V d A

R x 1 + R x 2 + p 1 A - p 2 A = u 1 - m ˙ + u 2 m ˙ = 0

R x 1 + R x 2 = A ( p 2 - p 1 )

E

r × F s = ∫ S C r × V   ρ V d A

r 1 × R x 1 + p 1 A î + r 2 × R x 2 - p 2 A î = r 1 × V 1 î   - m ˙ + r 2 × V 2 î   m ˙

Passo 3

Sendo:

r 2 = 0 ;

r 1 = L j ^ ,   e n t ã o   r 1 × î = - L k ^ .

Temos:

- L R x 1 + p 1 A k ^ = - L V 1 - m ˙ k ^

R x 1 = - ( S G ρ ) Q 2 A - p 1 A

Substituindo:

S G ρ = 0,95 ⋅ 1000 = 950   k g / m 3 ;

Q = 0,58   m 3 / s ;

A = π D 2 4 = π 0,25 2 4 = 0,049   m 2 ;

p 1 = 345   k P a .

Temos:

R x 1 = - 950 ⋅ 0,58 2 0,049 - 345 x 10 3 ⋅ 0,049 = - 23,4   k N

K x 1 = - R x 1 = 23,4   k N

Passo 4

Calculando R x 2 :

R x 2 = A p 2 - p 1 - R x 1

Sendo:

p 2 = 332   k P a .

Temos:

R x 2 = 0,049 ⋅ 332 - 345 + 23,4 = 22,8   k N

K x 2 = - R x 2 = - 22,8   k N

Passo 5

Calculando o Torque:

T = r × F S = r 1 × K x 1 i ^ = L j ^ × K x 1 î = - L R x 1 k ^

Sendo:

L = 20   m .

Temos:

T = - 20 ⋅ 23,4 = - 468   k N

Resposta

K x 1 = 23,4   k N

K x 2 = - 22,8   k N

T = - 468   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água a 20°C descarrega para atmosfera padrão (nível do mar) através do bocal divisor abaixo. As áreas das seções são A 1 = 0,02m 2 e A 2 = A 3 = 0,008m 2 . Se p 1 = 135k P a (absoluta) e vazão é Q 2 =
Gasolina a 20°C está escoando com V 1 = 12m / s em um tubo de 5 cm de diâmetro, quando encontra um trecho de 1 m de comprimento com sucção radial uniforme na parede. No final da região de sucção, a ve
Como mostra a Figura P3.90, uma coluna líquida de altura h é confinada em um tubo vertical de seção transversal A por um tampão. Em t = 0 , o tampão é repentinamente removido, expondo o fundo do líqui
Água a 20°C escoa em regime permanente através de uma curva com redução em um tubo, como mostra a Figura P3.77. As condições conhecidas são p 1 = 350k P a , D 1 = 25c m , V 1 = 2,2m / s , p 2 = 120k P
Uma camada bidimensional de água, com 10 cm de espessura e movendo-se a 7 m/s, colide com uma parede fixa inclinada 20° com relação à direção da camada. Considerando escoamento sem atrito, encontre (a