Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 76

Uma camada bidimensional de água, com 10 cm de espessura e movendo-se a 7 m/s, colide com uma parede fixa inclinada 20° com relação à direção da camada. Considerando escoamento sem atrito, encontre (a) a força normal à parede por metro de profundidade, e encontre as espessuras da camada de água defletida (b) a montante e (C) a jusante ao longo da parede.

Passo 1

Bora matar essa questão ai!

Vamos colocar um esqueminha para analisarmos melhor!

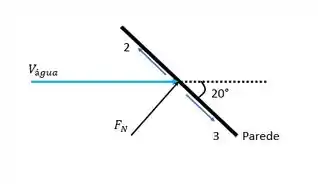
Vemos ai o jato de água dito, e, ao bater na parede inclinada ele se divide dando origem a uma corrente a montante (2) e a jusante (3).

Em (a) queremos saber a força normal à parede que, é devido ao momento do jato de água, assim:

∑ F N = - m ˙ u = - 1000 k g m 3 ⋅ 0,1   m 2 ⋅ ( 7   m / s ) ⋅ cos ⁡ 70 ° = 23,94   N / m

Passo 2

Em (b), queremos saber a espessura da camada de água defletida a montante. Considerando um escoamento sem atrito, teremos que a velocidade será a mesma, ou seja, V á g u a = V 2 = V 3 , assim:

V á g u a A 1 = V á g u a A 2 + V á g u a A 3

Logo,

A 2 = A 1 sen ⁡ θ → A 2 = 0,1   m ⋅ sen ⁡ 20 ° = 0,034   m ≈ 3   c m

Passo 3

Em (c), queremos saber a espessura do jato a jusante, assim, seguindo o mesmo raciocínio para (b):

A 3 = A 1 cos ⁡ θ = 0,1   m ⋅ cos ⁡ 20 ° = 0,094   m ≈ 9,4   c m

Resposta

  1. 23,94 N/m
  2. 3 cm
  3. 9,4 cm
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repeat Prob. P3.49 by assuming that p1 is unknown andusing Bernoulli’s equation with no losses. Compute thenew bolt force for this assumption. What is the head lossbetween 1 and 2 for the data of Prob
As a simpler approach to Prob. P3.96, apply the unsteadyBernoulli equation between 1 and 2 to derive a differentialequation for the motion z(t). Neglect friction and compressibility.
The waterwheel in Fig. P3.162 is being driven at 200 r/minby a 150-ft/s jet of water at 208C. The jet diameter is 2.5 in.Assuming no losses, what is the horsepower developed bythe wheel? For what spee
The horizontal lawn sprinkler in Fig. P3.149 has a waterflow rate of 4.0 gal/min introduced vertically through thecenter. Estimate (a) the retarding torque required to keepthe arms from rotating and (
Steam enters a horizontal turbine at 350 lbf/in2 absolute,5808C, and 12 ft/s and is discharged at 110 ft/s and 258Csaturated conditions. The mass fl ow is 2.5 lbm/s, and theheat losses are 7 Btu/lb of