Uma placa de alumínio altamente polida com comprimento de 0,5 m e largura de 0,2 m é submetida a uma corrente de ar a uma temperatura de 23°C e a uma velocidade de 10 m/s. Devido às condições a montante, o escoamento é turbulento ao longo de toda a extensão da placa. Uma série de aquecedores segmentados, controlados independentemente, está fixada à superfície inferior da placa com o objetivo de manter condições aproximadamente isotérmicas ao longo de toda a placa. O aquecedor elétrico, cobrindo a seção localizada entre x1 = 0,2 m e x2 = 0,3 m, é mostrado na figura.

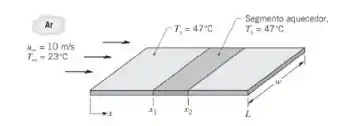
1. Estime a potência elétrica que deve ser fornecida ao segmento aquecedor identificado para manter a temperatura superficial da placa a Ts = 47°C.
2. se o soprador que mantém a velocidade da corrente de ar sobre a placa apresentar problemas, mas a potência nos aquecedores permanecer constante, estime a temperatura superficial do segmento identificado. Considere o ar ambiente infinito e quiescente, a 23°C.

Para resolver a letra a, precisamos usar a equação:

Vamos encontrar quem está faltando, beleza?

Vamos achar então primeiro quem é esse :

O número de Reynolds é dado por:

Substituindo isso na equação de :

Teremos então:

Fazendo o mesmo processo para o vamos ter:

então:

Agora sim podemos finalizar a letra a:

E ficaremos com:

Na letra b, precisamos da temperatura e vamos conseguir pela relação:

Precisamos desse , que vamos assumir como nosso coeficiente de convecção e achar assim:

Precisamos encontrar os fatores que faltam:

Esse :

E teremos:

Nosso será:

Agora sim vamos ter:

Agora simmmm! Podemos achar o que a letra b quer:

ou

Uhul!! Conseguimos!