Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 50

Certos projetos de fornos que queimam madeira se baseiam exclusivamente na transferência de calor por radiação e convecção natural para a vizinhança. Considere um forno que forma um compartimento cúbico, Lf = 1 m de lado, no interior de uma grande sala. As paredes externas do forno têm uma emissividade de ε = 0,8 e estão a uma temperatura de operação de Ts,f = 500 K.

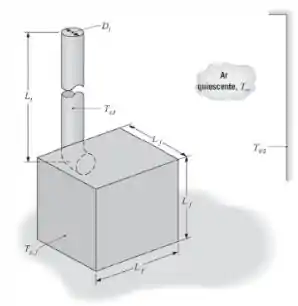
O tubo do forno, que pode ser considerado isotérmico a uma temperatura de operação de Ts,t = 400 K, tem diâmetro Dt = 0,25 m e altura Lt = 2 m, e se estende do forno até o teto. O forno encontra-se em uma grande sala cujo ar e as paredes estão a T∞ = Tviz = 300 K. Desprezando a transferência de calor na pequena seção horizontal do tubo e a troca de calor por radiação entre o tubo e o forno, estime a taxa de transferência de calor do forno e do tubo para o ar e a vizinhança.

Passo 1

Fala aí! Vamos fixar nossos conhecimentos resolvendo esse probleminha? Vamos nessa!

O enunciado quer que a gente encontre a transferência de calor total do sistema… Então vamos nessa!

Mas antes precisaremos de dados adicionais para o nosso cálculo, vamos encontrar eles no apêndice do livro, tabela A-4, assumindo um T f = 400   K :

k = 0,0338   W / m . K v = 26,41   .   10 - 6   m ² / s P r = 0,69

α = 38,3   .   10 - 6   m ² / s β = 0,0025   K - 1

E com um T f = 350   K :

k = 0,030   W / m . K v = 20,92   .   10 - 6   m ² / s P r = 0,70

α = 29,9   .   10 - 6   m ² / s β = 0,00286   K - 1

Vamos as continhas então!

Passo 2

Para resolver o que o enunciado quer, precisamos usar a equação:

q t o t = 4   .   q s   +   q t   +   q p

Vamos encontrar todos esses que estão faltando, beleza?

Vamos usar essas equações aqui:

q s = h _ s + h r a d ,   s   .   L s 2   .   T s ,   s - 300

q t = h _ t + h r a d ,   s   .   L s 2   .   T s ,   s - 300

q p = h _ p + h r a d ,   p   .   π   .   D p   .   L p   .   T p ,   s - 300

Tem várias coisas faltando aí, né? Vamos encontrar todas elas!

Passo 3

Vamos encontrar o h r a d ,   s :

h r a d ,   s = ε   .   σ   .   T s ,   s - T s u r   .   T s ,   s ² - T s u r ²

h r a d ,   s = 0,8   .   48   .   10 - 8   .   500 - 300   .   500 ² - 300 ²

h r a d ,   s = 12,3   W / m ² . K

Agora o h r a d ,   p :

h r a d ,   p = ε   .   σ   .   T s ,   p - T s u r   .   T s ,   p ² - T s u r ²

h r a d ,   p = 0,8   .   48   .   10 - 8   .   500 - 400   .   500 ² - 400 ²

h r a d ,   p = 7,9   W / m ² . K

Além disso vamos encontrar o R a L ,   s , R a L ,   t e o R a L ,   p :

R a L ,   s = g   .   β   .   T s ,   s - T ∞   .   L s 3 v   .   α R a L ,   t = g   .   β   .   T s ,   t - T ∞   .   A s P 3 v   .   α R a L ,   p = g   .   β   .   T s ,   p - T ∞   .   L p 3 v   .   α

R a L ,   s = 9,8   .   0,0025   .   400 - 300   .   1 3 20,92   .   10 - 6   .   29,9   .   10 - 6 R a L ,   t = 9,8   .   0,0025   .   500 - 300   .   0,025 3 20,92   .   10 - 6   .   29,9   .   10 - 6 R a L ,   p = 9,8   .   0,0025   .   100   .   2 3 20,92 . 10 - 6 . 29,9 . 10 - 6

R a L ,   s = 4,84   .   10 9 R a L ,   t = 7,57   .   10 7 R a L ,   p = 3,59   .   10 10

Passo 4

Agora vamos encontrar o N u _ L ,   s , N u _ L ,   t e o N u _ L ,   p :

N u _ L ,   s = 0,825 + 0,387   .   R a L ,   s 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2 N u _ L ,   p = 0,825 + 0,387   .   R a L ,   p 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

N u _ L ,   s = 0,825 + 0,387   .   4,84   .   10 9 1 / 6 1 + 0,492 0,69 9 / 16 8 / 27 2 N u _ L ,   p = 0,825 + 0,387   .   3,59   .   10 10 1 / 6 1 + 0,492 0,69 9 / 16 8 / 27 2

N u _ L ,   s = 199,9 N u _ L ,   p = 377,6

N u _ L ,   t = 0,15   .   R a L ,   t 1 / 3

N u _ L ,   t = 0,15   .   7,57   .   10 7 1 / 3

N u _ L ,   t = 63,5

E agora podemos achar:

h _ s = N u _ L ,   s   .   k L h _ t = N u _ L ,   t   .   k L h _ p = N u _ L ,   p   .   k L

h _ s = 199,9   .   0 ,   338 1 h _ t = 63,5   .   0,0338 1 h _ p = 377,6   .   0,0338 2

h _ s = 6,8   W / m ² . K h _ t = 8,6   W / m ² . K h _ p = 5,7   W / m ² . K

Passo 5

Agora simmmm! Podemos achar o que os termos começando pelo q s :

q s = 6,8 + 12,3   .   1 ²   .   500 - 300

q s = 3820   W

Agora o q t :

q t = 8,6 + 12,3   .   1 ²   .   500 - 300

q t = 4180   W

Estamos quase acabando, falta o q p :

q p = 5,7 + 7,9   .   π   .   0,25   .   2   .   400 - 300

q p = 2140   W

Show! Temos então:

q t o t = 4   .   3820   +   4180   +   2140

q t o t = 21600   W

Uhul!! Conseguimos!

Resposta

q t o t = 21600   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro de 12c m de diâmetro e 15m de comprimento com temperatura de superfície de 10° C é colocado horizontalmente no ar a 40° C . Calcule a taxa permanente de transferência de calor para os
Uma placa de ( 0,5m× 0,5m ) é inclinada em um ângulo de 30 ° . A superfície superior da placa é bem isolada. Estime a taxa de perda de calor da placa quando a superfície inferior é mantida a 60°
Considere uma placa horizontal L×L que é colocada em ar quente com a superfície quente para cima. Se a temperatura do filme é 20° C e o número de Nusselt médio em convecção natural é da forma
Considere o coletor solar de energia de uma placa plana colocada na horizontal no terraço de uma casa. O coletor tem 1,5m de largura e 4,5m de comprimento, e a temperatura média da superfície expost
Água quente está fluindo a uma velocidade média de 1,2m / s através de um tubo de ferro fundido ( k =52W / m ∙ ℃ ) ℃ cujos diâmetros interno e externo são 2,5c m e 3c m , respectivamente. O tubo p