Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 48
Uma placa fina está separada de duas placas fixas por líquidos muito viscosos com e , respectivamente, como mostra a Figura . Os espaçamentos e entre as placas não são iguais, como mostra a figura. A área de contato é entre a placa central e cada fluido.
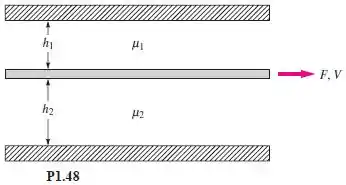
(a) Considerando uma distribuição linear de velocidade em cada fluido, deduza a força necessária para puxar a placa à velocidade .
(b) Existe necessariamente uma relação entre as duas viscosidades, e ?
Passo 1
Primeiro vamos fazer um esquema da nossa questão para ilustrar nosso problema:
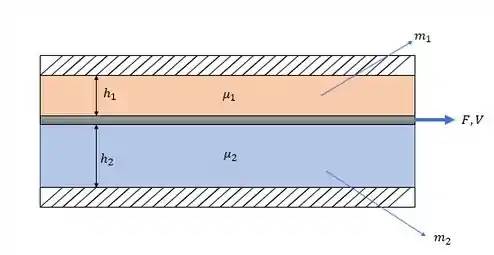
Nossa questão nos pede a dedução da força e a verificação de uma relação entre as viscosidades, bora resolver isso!
Passo 2
a)
Vamos assumir que a distribuição de velocidade é linear para os dois fluídos, para facilitar nosso trabalho!
Assim temos:
Vale lembrar que nossa formula só é válida para um escoamento laminar, não se aplicando a escoamento turbulento.
Passo 3
b)
Bem como a placa do centro separa ambos os fluídos, eles não têm contato direto.
Logo não existe nenhuma relação entre a viscosidade de ambos os fluídos!
Isso é tudo pessoal, essa foi rápida! \o/
Resposta
a)
b) Não existe relação entre as viscosidades.