Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 127

Seja uma placa delgada opaca e horizontal, com um aquecedor elétrico na sua superfície inferior. A superfície frontal está exposta ao ar ambiente a 20 ° C , com um coeficiente de transferência de calor por convecção de 10   W / ( m 2 · K ) , uma irradiação solar de 600   W / m 2 e uma temperatura do céu efetiva de – 40 ° C .

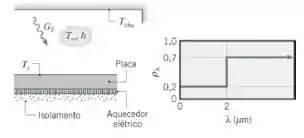
Qual é a potência elétrica ( W / m 2 ) necessária para manter a temperatura superficial da placa em T s =   60 ° C , sendo a placa difusa e com a refletividade hemisférica espectral mostrada na figura?

Passo 1

Oi oiii, vamos ver o que temos aqui? Nessa questão nós temos que uma placa horizontal opaca e espectralmente seletiva com aquecedor elétrico na parte traseira é exposta à convecção, irradiação solar e irradiação do céu, bem exposta ela né? hahah

A partir dessa exposição toda vamos encontrar a energia elétrica necessária para manter a placa a 60 ° C .

Passo 2

Para resolver essa questão vamos assumir que a placa é opaca, difusa e uniforme e que nenhum calor perdeu a parte traseira do aquecedor, show?!

A partir de um balanço energético no sistema de aquecimento de placas, por unidade de área de base,

E ˙ ' ' e n t - E ˙ ' ' s a i = 0

q e l e c ' ' + α s G s + α G a t m - ε E b T s - q c o n v ' ' =   0

Onde,

G a t m = σ T c e u 4

E b = σ T s 4

E,

q c o n v ' ' = h ( T s - T ∞ )

Passo 3

A absorção solar é,

α = ∫ 0 ∞ α λ G λ , s d λ ∫ 0 ∞ G λ , s d λ = ∫ 0 ∞ α λ E λ , b ( λ , 5800   K ) d λ ∫ 0 ∞ E λ , b ( λ , 5800   K ) d λ

Onde,

G λ , s ~ E λ , b ( λ , 5800   K )

Note que,

α λ =   1   -   ρ λ

α = ( 1 - 0,2 ) F 0 - 2 μ m + ( 1 - 0,7 ) 1 - F 0 - 2 μ m

Usando a tabela 12.1 para λ   T = 2 × 58 00 = 116 00 μ m . K ,   F ( 0 - λ   T ) = 0 , 941 . Então,

α = 0,8 × 0,941 + 0,3 1 - 0,941 = 0,771

Passo 4

A emissividade hemisférica total é,

ε = ( 1 - 0,2 ) F 0 - 2 μ m + ( 1 - 0,7 ) 1 - F 0 - 2 μ m

Em λ T   =   2   μ m   ×   333   K   =   666   K , encontramos F ( 0 - λ T )   ≈   0,000 . Então, ε   =   0,30 .

A capacidade de absorção hemisférica total para a irradiação do céu é,

α   =   ε   =   0,30

Pois, a superfície é cinza para esse processo de emissão e irradiação. Substituindo os valores numéricos temos,

q e l e c ' ' =   ε   σ T s 4 + h T s - T ∞ - α s G s - α σ T c e u 4

q e l e c ' ' = 0,30 × σ 333 K 4 + 10 W m 2 . K 60 - 20 ° C - 0,771 × 600 W m 2 - 0,30 × σ 2 33 K 4

q e l e c ' ' = 96,5   W / m 2

Com isso encontramos a potência elétrica necessária para manter a temperatura superficial da placa em T s =   60 ° C , que é o que o enunciado pedia. 😉

Resposta

q e l e c ' ' = 96,5   W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A asa de alumínio oxidado de um avião tem um comprimento de corda deL c =4m e uma emissividade hemisférica espectral caracterizada pela distribuição mostrada na figura.(a) Considere condições nas quai
Duas placas, uma com a superfície pintada de preto e a outra com um revestimento especial (cobre oxidado quimicamente), estão em órbita da Terra e estão expostas à radiação solar. Os raios solares faz
Um satélite esférico com diâmetro D encontra-se em órbita ao redor da Terra e é revestido por um material difuso, que tem absortividade espectral αλ = 0,6 para λ ≤ 3 μm e αλ = 0,3 para λ3 μm. Quando o
A absortividade direcional de uma superfície cinza varia com θ como a seguir. Qual é a razão entre a absortividade normal αn e a emissividade hemisférica da superfície? Considere uma placa com essas c