A asa de alumínio oxidado de um avião tem um comprimento de corda de e uma emissividade hemisférica espectral caracterizada pela distribuição mostrada na figura.

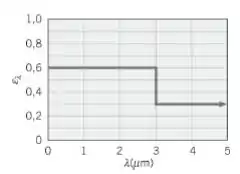
(a) Considere condições nas quais o avião está em terra onde a temperatura do ar é de , a irradiação solar é de e a temperatura do céu efetiva é de . Se o ar estiver quiescente, qual é a temperatura da superfície superior da asa? A asa pode ser aproximada por uma placa plana horizontal.

(b) Quando o avião está voando a uma altitude de aproximadamente e a uma velocidade de , a temperatura do ar, a irradiação solar e a temperatura do céu efetiva são e , respectivamente. Qual é a temperatura da superfície superior da asa? As propriedades do ar podem ser aproximadas por e .

Para resolver essa questão vamos levar em conta algumas considerações, mas fica tranquilo que a gente entende elas juntos, ta bem?! As considerações são:

(1) Estado estacionário;

(2) Transferência de calor desprezível da parte traseira da superfície da asa;

(3) Comportamento difuso da superfície;

(4) Radiação solar desprezível para

(5) Radiação negligenciável do céu e emissão de superfície para

(6) Ar quiescente para condição do solo;

(7) Folha de ar pode seja aproximado como uma placa plana;

(8) Aquecimento viscoso desprezível na camada limite para a condição de voo;

(9) A extensão da asa é muito maior que o comprimento do acorde ;

(10) Na transição em voo o número de Reynolds é .

Pronto! Agora já temos tudo o que é preciso para, de fato, iniciar. 😊

Para condições de solo e de voo, um balanço energético da superfície gera,

Onde,

Para a condição do solo, pode ser avaliado a partir da Eq. 9.30 ou 9.31, onde,

Usando o software IHT para resolver a equação do Passo 1 e considerando o efeito das propriedades dependentes da temperatura, a temperatura da superfície é,

Onde,

e

Com isso, a transferência de calor da superfície por emissão e convecção é de e , respectivamente.

Para a condição de voo,

Para condições da camada limite mista, laminar / turbulenta (capítulo 7) e um número de Reynolds de transição de ,

Substituindo na equação do Passo 1, uma solução de tentativa e erro produz,

E a transferência de calor da superfície por emissão e convecção agora é de e , respectivamente.