Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 14

Uma placa em liga de alumínio ( 2024 ) , aquecida até uma temperatura uniforme de 227 ° C , é resfriada enquanto permanece suspensa em posição vertical em uma sala cujo ar ambiente e a vizinhança se encontram a 27 ° C . A placa é quadrada, com   0,3   m de lado e 15   m m de espessura. Sua emissividade é de 0,25 .

(a) Desenvolva uma expressão para a taxa de variação da temperatura da placa com o tempo, admitindo que a temperatura seja uniforme em qualquer tempo.

(b) Determine a taxa inicial de resfriamento ( K / s ) , quando a temperatura da placa é de 227 ° C .

(c) Justifique a hipótese de temperatura uniforme na placa.

(d) Calcule e represente graficamente o histórico da temperatura da placa de t   =   0 até o tempo necessário para ela atingir a temperatura de 30 ° C . Calcule e represente graficamente as variações correspondentes nas taxas de transferência de calor convectiva e radiante.

Passo 1

Nessa questão nós temos uma placa de liga de alumínio ( 2024 ) a uma temperatura uniforme inicial de 227   °   C suspensa em uma sala onde o ar ambiente e os arredores estão a 27   °   C . Ilustrativamente,

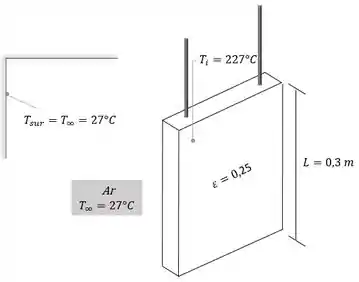
A partir disso queremos encontrar a expressão da taxa de variação temporal da placa, a taxa inicial de resfriamento ( K   /   s ) quando a temperatura da placa é 227 ° C e saber a validade ao assumir uma temperatura uniforme da placa. Vamos lá!

Passo 2

Para resolver essa questão vamos assumir: temperatura da placa uniforme, ar ambiente quieto e extenso e arredores grandes em comparação com a placa. Além disso, temos que as propriedades da placa serão retiradas da Tabela A.1 para T f = 400 K ,   1   a t m .

De um balanço energético na placa com convecção e troca de radiação livres,

- E ˙ s a i = E ˙ s t

Nós obtemos,

- h L - 2 A s T s - T ∞ - ε 2 A s σ T s 4 - T s u r 4 = ρ A s t c d T d t

Ou,

d T d t = - 2 ρ t c - h L - T s - T ∞ - ε σ T s 4 - T s u r 4

Onde T s , a temperatura da placa, é assumida como uniforme a qualquer momento.

Passo 3

Para avaliar ( d T   d t ) , devemos estimar h L - . Mas primeiro, vamos encontrar o número de Rayleigh,

R a L = g β ( T s - T ∞ ) L 3 ν α

Substituindo os valores temos,

R a L = 9,8 m s 2 1 4 00 K ( 227 - 27 ) K 0 , 3 m 3 26,41 × 10 - 6 m 2 s 38,3 × 10 - 6 m 2 s = 1 , 308 × 10 8

Como R a L < 10 9 , o fluxo é laminar e,

N u L - = h L - L k = 0,68 + 0,670   R a L 1 4 1 + 0,492 P r 9 16 4 9

Substituindo os valores,

h L - = 0,03 38 W m . K 0,30 m 0,68 + 0,670   ( 1,308 × 10 8 ) L 1 4 1 + 0,492 0 , 690 9 16 4 9

h L - = 6,2 5 W m 2 . K  

Passo 4

Agora, podemos substituir os valores encontrados na expressão do Passo 2 e encontrar d T / d t   ,

d T d t = - - 2 2 770 k g m 3 ×   0,015 m × 9 83 J k g . K ×

6,25 W m 2 . K 227 - 27 K + 0,25 5,67 × 10 - 8 W m 2 . K 4 5 00 4 - 300 4 K 4

d T d t = - 0,099   K / s

Passo 5

A suposição da temperatura uniforme é justificada se o critério do número de Biot for atendido. Com,

L c ≡ V 2 A s = A s t 2 A s = t 2

E,

h - t o t = h - c o n v + h - r a d

B i = h - t o t t 2 k ≤ 0,1

Usando a relação do coeficiente de radiação linearizada, encontramos,

h - r a d = ε σ T s + T s u r T s 2 + T s u r 2

Substituindo os valores,

h - r a d = 0,25 5,67 × 10 - 8 W m 2 . K 4 500 + 300 5 00 2 + 300 2 K 3 = 3,86 W m 2 . K

Portanto,

B i   = 6,25   +   3,86 W m 2   ⋅ K   0,015 m 2 186   W / m ⋅ K   =   4,07   ×   1 0 - 4

Como B i   < <   0,1 , a suposição é apropriada.

Resposta

  1. d T d t = - 2 ρ t c - h L - T s - T ∞ - ε σ T s 4 - T s u r 4
  2. d T d t = - 0,099   K / s
  3. Como B i   < <   0,1 , a suposição é apropriada.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma grade de aquecimento circular, com diâmetro de 0,25 m e emissividade de 0,9, é mantida a uma temperatura superficial constante de 130°C. Qual é a potência elétrica necessária quando o ar ambiente
Bebidas em lata, com 150 mm de comprimento por 60 mm de diâmetro, encontram-se inicialmente a uma temperatura de 27°C e devem ser resfriadas pela sua colocação em uma geladeira a 4°C. Com o objetivo d
Um espaço de ar com 50 mm de espessura separa duas placas de metal horizontais que formam a superfície superior de um forno industrial. A placa inferior está a Tq = 200°C e a placa superior a Tf = 50°
Coeficientes de transferência de calor por convecção para uma superfície horizontal aquecida voltada para cima podem ser determinados por um sensor cujas características específicas dependem se a temp
Considere o Problema 8.47. Uma solução mais realista levaria em consideração a resistência à transferência de calor devido à convecção natural na parafina durante o processo de liquefação. Admitindo q