Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 93

Um espaço de ar com 50 mm de espessura separa duas placas de metal horizontais que formam a superfície superior de um forno industrial. A placa inferior está a Tq = 200°C e a placa superior a Tf = 50°C. O operador da planta deseja colocar um isolamento entre as placas para minimizar a perda térmica. As temperaturas relativamente altas impedem o uso de materiais isolantes na forma de espumas ou feltros. Materiais isolantes com vácuo não podem ser usados em função do ambiente industrial hostil e do seu custo. Um jovem engenheiro sugere que folhas de alumínio horizontais, muito finas e igualmente espaçadas, podem ser inseridas no espaço para eliminar a convecção natural e minimizar a perda térmica através do espaço de ar.

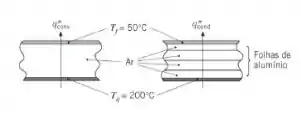
  1. Determine a perda térmica por convecção através do espaço quando não há isolamento.
  2. Determine o número mínimo de folhas que deve ser inserido no espaço para eliminar a convecção natural.
  3. Determine o fluxo térmico condutivo através do espaço de ar com as folhas de alumínio no lugar.

Passo 1

Fala aí! Vamos fixar nossos conhecimentos resolvendo esse probleminha? Vamos nessa!

O enunciado quer que a gente resolva essas três letrinhas… Então vamos dar isso a ele!

Opa! Precisaremos de dados adicionais para o nosso cálculo, vamos encontrar eles no apêndice do livro, tabela A-4, assumindo um T f = T s + T ∞ / 2 :

k = 0,03365   W / m . K v = 26,19   .   10 - 6   m ² / s

α = 3,796   .   10 - 5   m ² / s P r = 0,6904

Vamos as continhas então!

Passo 2

Para resolver a letra a, precisamos encontrar a perda térmica por convecção, para isso precisamos encontrar o h _ L , e para achar ele precisamos saber antes, o R a :

R a = g   .   β   .   T h - T c   .   L ³ v   .   α

R a = 9,8   .   1 ( 125 + 273 )   .   200 - 50   .   ( 0,05 ) ³ 2,619   .   10 - 5   .   3,796   .   10 - 5

R a = 4,64   .   10 5

E agora teremos o nosso h _ L :

h _ L = 0,069   .   k L   .   R a 1 / 3   .   P r 0,074

h _ L = 0,069   .   0,03365 5   .   10 - 3   .   4,64   .   10 5 1 / 3   .   ( 0,6904 ) 0,074

h _ L = 3,50   W / m ² . K

Aí sim! Agora é só achar o que ele quer:

q c o n v " = h _ L   .   T h - T c

q c o n v " = 3,50   .   200 - 50

q c o n v " = 525   W / m ²

Primeira parte ok!

Passo 3

A letra b, quer que a gente encontre o número de folhas… Para isso vamos usar a seguinte relação, como R a L g < 1708 , vamos ter que:

L g = L N + 1

Então vamos substituir isso na equação que usamos do R a :

R a L g = g   .   β   .   T h - T c   .   N + 1 .   L N + 1 ³ v   .   α < 1708

9,8   .   1 ( 125 + 273 )   .   200 - 50   .   N + 1 .   0,05 N + 1 ³ 2,619   .   10 - 5   .   3,796   .   10 - 5 < 1708

N > 3,06

Então nosso número de folhas será:

N = 4

Passo 4

Pra fechar vamos resolver a letra c! Que quer o fluxo térmico condutivo:

q c o n d " =   k   .   T h - T c L

q c o n d " =   0,03365   .   200 - 50 0,05

q c o n d " =   101   W / m ²

Uhul! Conseguimos!!

Resposta

  1. q c o n v " = 525   W / m ²

  2. N = 4

  3. q c o n d " =   101   W / m ²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dissipadores de calor de alumínio com perfil retangular são comumente usados ​​para resfriar componentes eletrônicos. Considere um dissipador de calor de 7,62 cm de comprimento e 9,68 cm de largura cu
Uma placa de 10c m × 10c m tem uma temperatura de superfície constante de 150°C. Determine o número de Grashof se o chip for colocado nos seguintes fluidos: Ar (1 atm, 30°C); Água líquida (30°C);Óleo
Por que dissipadores de calor com aletas estreitamente compactas não são adequados para a transferência de calor por convecção natural, apesar de aumentarem a superfície de transferência de calor?
Reconsidere o dissipador de calor do Problema 9-58. A fim de reforçar a transferência de calor, uma cobertura (placa fina metálica retangular) cuja superfíce é igual à área da base do dissipador de ca
Uma superfície de uma placa de rua 0,2m × 0,2m tem absorvidade de 0,6 e emissividade de 0,7. A radiação solar é incidente na placa de rua a uma taxa de 200 W m 2 , e o ar ao redor é de 25°C. Determine