Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 102

Uma placa com parede delgada separa o interior de um grande forno da sua vizinhança, que se encontra a 300   K . A placa é feita com um material cerâmico cujo comportamento da superfície pode ser considerado difuso. A superfície exterior da placa é resfriada pelo ar. Com o forno operando a 2400   K , a convecção na superfície interior da placa pode ser desprezada.

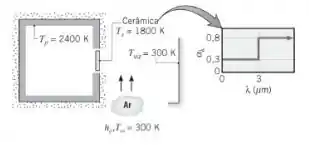
(a) Se a temperatura na placa cerâmica não pode exceder 1800   K , qual é o valor mínimo do coeficiente de transferência de calor por convecção na superfície externa da placa, h e , que deve ser mantido pelo sistema de resfriamento por ar?

(b) Calcule e represente graficamente a temperatura da placa como uma função do coeficiente externo de transferência de calor por convecção h e para 50   ≤   h e   ≤   250   W / ( m 2 · K ) .

Passo 1

Nessa questão nós temos que as temperaturas do forno e arredores separadas por placa cerâmica e a temperatura máxima admissível e capacidade de absorção espectral da placa. Com isso vamos encontrar o valor mínimo do coeficiente de convecção do lado do ar, h e .

Passo 2

Para resolver essa questão nós vamos:

(1) Superfície difusa;

(2) Gradientes de temperatura desprezíveis na placa;

(3) Convecção interna desprezível;

(4) O forno e o ambiente agem como corpos negros.

A partir de um balanço de energia superficial na placa,

α w G w + α s u r G s u r = 2 E + q c o n v ' '

Então,

α w σ T w 4 + α s u r σ T s u r 4 = 2 ε σ T s 4 + h e T s - T ∞

h e = α w σ T w 4 + α s u r σ T s u r 4 - 2 ε σ T s 4 T s - T ∞

Passo 3

Avaliando as absorptividades e emissividade,

α = ∫ 0 ∞ α λ G λ d λ G = ∫ 0 ∞ α λ E λ , b ( T w ) d λ E b ( T w )

α = 0,3 F ( 0 → 3 μ m ) + 0,8 1 - F 0 → 3 μ m

Usando a tabela 12.1 para λ   T w = 3 × 2400 = 72 00 μ m . K ,   F ( 0 → 3 μ m ) = 0 , 819 . Então,

α = 0,391

Como T s u r =   300   K , a irradiação dos arredores está em comprimentos de onda bem acima de 3   μ m . Então,

α s u r = ∫ 0 ∞ α λ E λ , b ( T s u r ) d λ E b ( T s u r ) ≈ 0,800

Passo 4

A emissividade é,

ε = ∫ 0 ∞ ε λ E λ , b T s d λ E b T s

ε = 0,3 F ( 0 → 3 μ m ) + 0,8 1 - F 0 → 3 μ m

Usando a tabela 12.1 para λ   T s = 5 400 μ m . K ,   F ( 0 → 3 μ m ) = 0 , 680 . Então,

ε = 0,460

Para o valor máximo permitido de T s   =   1800   K , segue-se que,

h e = 126 W m 2 . K

Resposta

  1. h e = 126 W m 2 . K
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas placas paralelas muito grandes são mantidas em temperaturas uniformes T 1 =750K e T 2 =500K e têm emissividades ε 1 =0,85 e ε 2 =0,7 . Se uma fina folha de alumínio com a mesma emissividade de
Um disco negro plano de 70c m de diâmetro é colocado no centro da superfície superior de uma caixa negra de 1m×1m×1m . Considerando que a temperatura da caixa é 620° C e a temperatura do disco é
Considere um forno cúbico de 3 m × 3 m × 3 m . A superfície de base do forno é negra e tem temperatura de 550K . As radiosidades para as superfícies superior e laterais são calculadas como sendo
Considere um forno cúbico de 3 m × 3 m × 3 m . A superfície da base do forno é negra e tem temperatura de 400K . As radiosidades para as superfícies superior e laterais são calculadas como sendo
Duas esferas concêntricas são mantidas em temperaturas uniformes T 1 =45° C e T 2 = 280° C e têm emissividades ε 1 = 0,25 e ε 2 =0,7 , respectivamente. Se a razão entre os diâmetros é D 1 D 2 =0