Uma placa plana fina quadrada de vidro que tem 1 m de lado, separa duas salas, uma com ar quiescente a 20°C e outra também com ar quiescente, porém a -20°C. As paredes da sala estão respectivamente à e . O vidro tem uma emissividade de 1. Qual deve ser sua temperatura? Qual é a taxa de calor que atravessa o vidro?
Passo 1
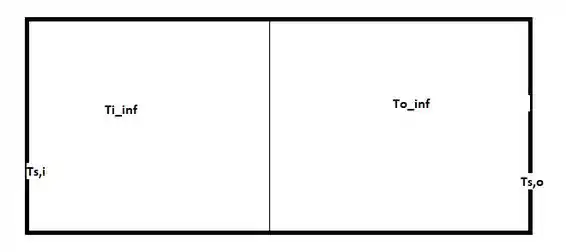
Note que o enunciado nos disse que o vidro é muito fino, então é como se ele não tivesse nem resistência de condução. Então aqui podemos aplicar um conceito de circuito térmico, certo?
E como já sabemos, em circuito térmico temos que o fluxo em uma placa plana é constante em qualquer parte do nosso circuito, ou seja:
Passo 2
Note que para resolver nosso problema, precisamos apenas encontrar o valor dos coeficientes convectivos de cada um dos ambientes acima.
A equação que usamos é
Para o ar a 20°C, temos as seguintes propriedades:
Para o ar a -20°C aproximadamente, temos:
Passo 3
Vamos agora calcular o valor de Ra para cada um dos ambientes
Note que precisamos ainda da temperatura do vidro, ou seja, não tem como resolver esse Ra aí, mas podemos pegar ele e substituir diretamente na equação de h que encontramos no passo (2) e assim termos e como função da temperatura do vidro!
Passo 4
Note que agora temos uma equação onde nossa única variável é a temperatura do vidro! Sim, ela é uma equação bem feinha de se resolver, porém note que é de extrema importância entender que os valores de propriedades termofísicas que você vai usar do lado esquerdo é para o ar na temperatura de 20°C e do lado direito em -20°C.
Bem, a partir daqui é “contarada” que você vai precisar fazer, e ao final vai obter uma temperatura do vidro aproximadamente de 5°C
E bem, agora que conhecemos a temperatura do vidro, podemos calcular a taxa que atravessa a nossa superfície vítrea, uma vez que teremos uma troca de calor dela com o ar por convecção: