Placas de circuitos são montadas nas paredes verticais interiores de um duto retangular de altura e comprimento . Embora as placas sejam resfriadas pela transferência de calor por convecção forçada para o ar que escoa através do duto, nem todo o calor dissipado pelos componentes eletrônicos é transferido para o escoamento. Parte do calor é transferida por condução através das paredes verticais do duto e então por convecção natural e radiação para o ar ambiente (atmosférico) e a vizinhança, que estão a uma mesma temperatura igual a . As paredes são metálicas e, em uma primeira aproximação, podem ser consideradas isotérmicas e a uma temperatura .

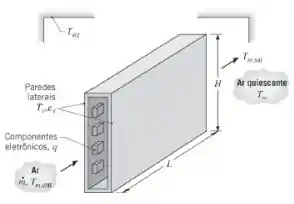
(a) Considere condições nas quais os componentes eletrônicos dissipam e o ar entra no duto a uma vazão de, a uma temperatura de . se a emissividade das paredes laterais for igual a e a temperatura de saída do ar igual a , qual é a temperatura da superfície ?

(b) Para reduzir a temperatura dos componentes eletrônicos, deseja-se intensificar a transferência de calor saindo das paredes laterais. Supondo que as condições no escoamento do ar permaneçam inalteradas, qual é o efeito na da aplicação de um revestimento com alta emissividade nas paredes laterais externas?

(c) Se houver a perda do escoamento do ar enquanto a potência continua sendo dissipada, qual é o valor resultante de para e ?

Para resolver a questão vamos assumir:

(1) Estado estacionário;

(2) Transferência de calor desprezível das superfícies superior e inferior do duto;

(3) Paredes laterais isotérmicas;

(4) Ambientes amplos;

(5) Líquido refrigerante é um líquido incompressível com dissipação viscosa desprezível;

(6) Propriedades constantes e retiradas da Tabela A.4.

O calor dissipado pelos componentes é transferido por convecção forçada ao líquido de refrigeração bem como por convecção natural e radiação para o ar ambiente e os arredores. Então,

Onde,

O valor de é obtido com o número de Rayleigh,

E,

Substituindo os valores encontrados com obtemos,

E as taxas de calor correspondentes são e.

Para e , temos:

Com e

Portanto, a emissão aprimorada da superfície produz uma temperatura operacional mais baixa e a transferência de calor pela radiação agora excede a causada pela condução.

Com a perda de fluxo do líquido de arrefecimento, podemos esperar que todo o calor seja dissipado pelas paredes laterais E obtemos,

,

,

Como a temperatura dos componentes eletrônicos excede a das paredes laterais, o valor de correspondente a pode ser inaceitável, caso em que o revestimento de alta emissividade deve ser aplicado às paredes.