Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 8
Uma placa plana, com largura de , é mantida a uma temperatura superficial uniforme de pelo uso de módulos retangulares geradores de calor, com espessura e comprimento , que são controlados independentemente. Cada módulo encontra-se isolado de seus vizinhos, bem como em sua superfície inferior. Ar atmosférico a escoa sobre a superfície da placa a uma velocidade de . As propriedades termofísicas dos módulos são , e .
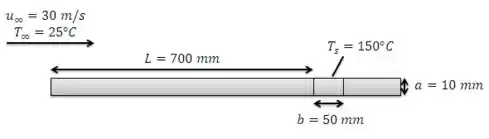
(a) Determine a geração de energia necessária, , em um módulo posicionado a uma distância de da aresta frontal.
(b) Determine a temperatura máxima neste módulo de geração.
Passo 1
No item (a) devemos determinar a energia gerada pelo módulo a de distância do início da placa. Para começar, vamos aplicar um balanço de energia para a superfície do módulo em contato com o ar:
Assumindo regime permanente e que só há perda de energia por convecção, ficamos com:
Precisamos então, determinar o coeficiente convectivo para a região em que o módulo está inserido. Tudo bem?
Para escolher a correlação mais adequada, vamos começar verificando o regime de escoamento. Para isso, vamos calcular o número de Reynolds:
Mas antes, precisaremos das propriedades do ar na temperatura de filme. Então:
Nesta temperatura, pela tabela A-4 do apêndice A temos que:
Passo 2
Voltando para o cálculo do número de Reynolds:
Para placa plana, indica que o regime de escoamento é turbulento.
Continuando, como o regime é turbulento, é razoável fazermos a aproximação:
em que
É a distância média entre o início e o fim do módulo da aresta da placa. Recalculando o número de Reynolds:
A correlação para o coeficiente convectivo local para uma placa plana, em regime turbulento é:
Vamos agora aplicar este valor na nossa equação do balanço de energia.
Passo 3
Vamos para o item (b). Devemos encontrar a temperatura máxima do módulo. Sabemos que a parede inferior é isolada, então não há fluxo de condução através dela. Certo?
Então, sabemos que o ponto em que ocorre a máxima temperatura é em .
Na seção 3 do livro temos que o perfil de temperaturas para uma placa plana com geração de energia é:
Então:
Resposta
(a) .
(b) .