Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 1

Considere os fluidos a seguir a uma temperatura de filme de 300   K , em escoamento paralelo sobre uma placa plana com uma velocidade de 1   m / s : ar atmosférico, água, óleo de motor e mercúrio.

(a) Para cada fluido, determine as espessuras das camadas-limite de velocidade e térmica a uma distância de 40   m m da aresta frontal.

(b) Para cada um dos fluidos especificados e nas mesmas coordenadas, represente em um gráfico as espessuras das camadas-limite em função da distância da aresta frontal em uma placa com 40   m m de comprimento.

Passo 1

O item (a) nos pede para determinar as espessuras das camadas limites térmica e de velocidade para quatro fluidos diferentes, na temperatura T = 300   K , escoando com velocidade v = 1   m / s .

Considerando regime laminar as camadas limites podem ser calculadas por:

δ = 5 x R e x 1 / 2

E

δ T = δ P r 1 3

Como as espessuras dependem dos adimensionais R e e P r vamos começar buscando as propriedades de cada fluido na temperatura de 300   K . De acordo com as tabelas A-4, A-5 e A-6 do apêndice A:

ϑ a r = 15,89 × 10 - 6   m 2 / s

P r ⁡ ( a r ) = 0,707

ϑ ó l e o = 550 × 10 - 6   m 2 / s

P r ⁡ ( ó l e o ) = 6400

ϑ H g = 0,1125 × 10 - 6   m 2 / s

P r ⁡ ( H g ) = 0,0248

ϑ H 2 O = 855 × 10 - 6 × 1,003 × 10 - 3 = 8,576 × 10 - 7   m 2 / s

P r ⁡ ( H 2 O ) = 5,83

Passo 2

Vamos começar calculando as espessuras das camadas limite para o ar. O primeiro passo é calcular o número de Reynolds:

R e x = v x ϑ

R e x = 1 × 40 × 10 - 3 15,89 × 10 - 6

R e x = 2517,3

Aplicando este valor na equação de camada limite de velocidade:

δ = 5 x R e 1 / 2

δ = 5 × 40 × 10 - 3 2517,3 1 / 2

δ = 3,986 × 10 - 3   m

Aplicando este resultado na fórmula de espessura da camada limite térmica:

δ T = δ P r 1 3

δ T = 3,986 × 10 - 3 ( 0,707 ) 1 3

δ T = 4,475 × 10 - 3   m

Passo 3

Iremos agora utilizar o mesmo procedimento para determinar as espessuras das camadas limite para o óleo de motor. Começando com o número de Reynolds:

R e x = v x ϑ

R e x = 1 × 40 × 10 - 3 550 × 10 - 6

R e x = 72,7

Aplicando este valor na equação de camada limite de velocidade:

δ = 5 x R e 1 / 2

δ = 5 × 40 × 10 - 3 72,7 1 / 2

δ = 23,452 × 10 - 3   m

Aplicando este resultado na fórmula de espessura da camada limite térmica:

δ T = δ P r 1 3

δ T = 23,452 × 10 - 3 ( 6400 ) 1 3

δ T = 1,263 × 10 - 3   m

Passo 4

Repetindo o mesmo procedimento para o mercúrio, começaremos calculando o número de Reynolds:

R e x = v x ϑ

R e x = 1 × 40 × 10 - 3 0,1125 × 10 - 6

R e x = 3,556 × 10 5

Aplicando este valor na equação de camada limite de velocidade:

δ = 5 x R e 1 / 2

δ = 5 × 40 × 10 - 3 3,556 × 10 5 1 / 2

δ = 0,335 × 10 - 3   m

Aplicando este resultado na fórmula de espessura da camada limite térmica:

δ T = δ P r 1 3

δ T = 0,335 × 10 - 3 ( 0,0248 ) 1 3

δ T = 1,15 × 10 - 3   m

Passo 5

Por fim, vamos calcular as espessuras das camadas limites para a água líquida:

R e x = v x ϑ

R e x = 1 × 40 × 10 - 3 8,576 × 10 - 7

R e x = 4,664 × 10 4

Aplicando este valor na equação de camada limite de velocidade:

δ = 5 x R e 1 / 2

δ = 5 × 40 × 10 - 3 4,664 × 10 4 1 / 2

δ = 0,926 × 10 - 3   m

Aplicando este resultado na fórmula de espessura da camada limite térmica:

δ T = δ P r 1 3

δ T = 0,926 × 10 - 3 ( 5,83 ) 1 3

δ T = 0,515 × 10 - 3   m

Passo 6

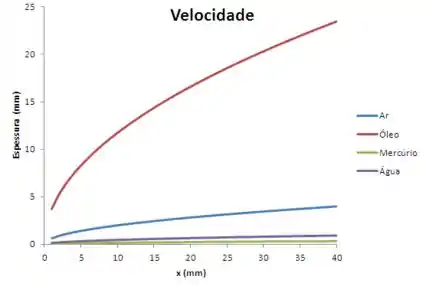
Vamos agora para o item (b). Ele nos pede para desenhar um gráfico de espessura das camadas limites em função da distância para os mesmos fluidos do item (a). Para isso vamos começar definindo uma equação geral para a espessura da camada limite em função de x :

δ = 5 x R e 1 / 2

δ = 5 x v x ϑ 1 / 2

δ = 5 ϑ v 1 / 2 x 1 / 2

E para espessura da camada limite térmica

δ T = δ P r 1 3

δ T = 5 ϑ v 1 / 2 P r 1 3 x 1 / 2

Com auxílio de Excel, ou outro programa gráfico, podemos plotar as curvas de espessura para diversos valores de x . Devemos obter algo da forma:

Resposta

(a) Ar:

δ = 3,986 × 10 - 3   m

δ T = 4,475 × 10 - 3   m

Óleo de motor:

δ = 23,452 × 10 - 3   m

δ T = 1,263 × 10 - 3   m

Mercúrio:

δ = 0,335 × 10 - 3   m

δ T = 1,15 × 10 - 3   m

Água:

δ = 0,926 × 10 - 3   m

δ T = 0,515 × 10 - 3   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa de cobertura de um coletor solar plano encontra-se a 15 °C, enquanto ar ambiente a 10 °C escoa paralelamente a sua superfície superior com uma velocidade u ∞ = 2 m/s.(a) Qual é a taxa de perda
No Problema 7.23, um projeto de um anemômetro foi analisado e a hipótese de temperatura na tira uniforme foi feita. Essa é uma boa hipótese quando o coeficiente de transferência de calor é baixo ou a
Uma placa plana de largura 1 m e comprimento 0,2 m é mantida a temperatura de 32 °C. Fluido ambiente a 22 °C escoa através da superfície superior da placa em escoamento paralelo. Determine o coeficien
Considere o aparelho fotovoltaico concentrador do Problema 7.19. O aparelho deve ser instalado em um ambiente desértico, de modo que o espaço entre as lentes concentradoras e o topo da célula fotovolt
Calcule o valor do coeficiente de transferência de calor médio para a placa do Problema 7.21 quando a placa inteira é rodada de 90°, de modo que metade da aresta frontal fica constituída pela porção l