Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 15
Explique sob quais condições a taxa de transferência de calor total em uma placa plana isotérmica com dimensões seria a mesma, independentemente do fato do escoamento paralelo sobre a placa ser direcionado ao longo do lado com comprimento ou do lado com comprimento . Com um número de Reynolds crítico de , para quais valores de a taxa de transferência de calor total seria independente da orientação?
Passo 1
Fala galera!!
Podemos desenhar o seguinte esquema para transferência de calor na placa plana de dimensões .
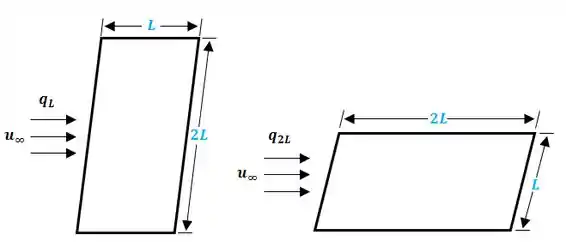
Para resolver essa questão, é bom ter em mente que a área da placa plana em ambas as orientações é igual, dessa forma, se os coeficientes de convecção de ambas as orientações forem iguais
a taxa total de transferência de calor será a mesma
Aqui, é a taxa de transferência de calor no escoamento em e é a taxa de transferência de calor no escoamento em , é o coeficiente de convecção médio para o escoamento em e é o coeficiente de convecção médio para o escoamento em .
Passo 2
Temos dois casos possíveis nesse que podem acontecer. Caso (a): Existe fluxo laminar na placa mais curta, enquanto existem condições de fluxo mistas na placa mais longa. Caso (b): Existem condições mistas da camada limite em ambas as placas. É impossível satisfazer o requisito de que, para o fluxo laminar sobre as duas placas.
Nos dois casos, é necessário que
e
Passo 3
Caso (a)
Para a condição de fluxo laminar na placa onde o escoamento ocorre em , podemos escrever a relação para o coeficiente médio de convecção da placa plana da seguinte maneira:
Aqui, é o número de Reynolds para a chapa plana com escoamento em e é o número de Prandtl, é o número médio de Nusselt para a chapa plana com escoamento em , é a condutividade térmica do ar e é o comprimento da chapa plana.
Passo 4
Agora, vamos escrever a relação para o coeficiente médio de convecção da placa plana onde o escoamento ocorre em para a condição de fluxo misto.
Aqui, é o número de Reynolds para a placa plana com escoamento em e é o número de Prandtl, é o número médio de Nusselt para a placa plana com escoamento em , é a condutividade térmica do ar e comprimento da placa plana.
Passo 5
Agora, vamos igualar os dois coeficientes médio de convecção devido a nossa afirmação feita no passo 1. Assim temos:
Agora, podemos substituir por na equação acima. Assim temos:
Como e , temos que está no intervalo de
Usando o método iterativo de Newton-Raphson
Onde posemos dizer que
Aplicando o método iterativo com qualquer valor dentro do intervalo, vamos encontrar que:
Portanto, a taxa de transferência de calor total será independente da orientação no caso a quando .
Passo 6
Caso (b)
Para a condição da camada limite mistas na placa onde o escoamento ocorre em , podemos escrever a relação para o coeficiente médio de convecção da placa plana da seguinte maneira:
Aqui, é o número de Reynolds para a chapa plana com escoamento em e é o número de Prandtl, é o número médio de Nusselt para a chapa plana com escoamento em , é a condutividade térmica do ar e é o comprimento da chapa plana.
Passo 7
Agora, vamos escrever a relação para o coeficiente médio de convecção da placa plana onde o escoamento ocorre em para a condição de fluxo misto.
Aqui, é o número de Reynolds para a placa plana com escoamento em e é o número de Prandtl, é o número médio de Nusselt para a placa plana com escoamento em , é a condutividade térmica do ar e comprimento da placa plana.
Passo 8
Agora, vamos igualar os dois coeficientes médio de convecção devido a nossa afirmação feita no passo 1. Assim temos:
Agora, podemos substituir por na equação acima. Assim temos:
Portanto, a taxa de transferência de calor total será independente da orientação no caso b quando .