Seja o escoamento sobre uma placa plana no qual se deseja determinar o coeficiente de transferência de calor médio em uma pequena seção entre e , , sendo .

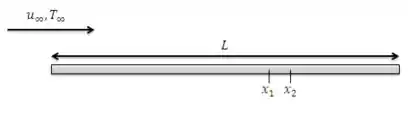
Forneça três expressões diferentes que possam ser usadas para determinar em termos (a) do coeficiente local em , (b) dos coeficientes locais em e em , e (c) dos coeficientes médios em e . Indique qual das expressões é aproximada. Considerando as possibilidades de escoamento laminar, turbulento ou misto, indique quando o uso de cada uma das equações é apropriado ou não.

Agora no item (b) precisamos expressar o coeficiente médio em termos dos coeficientes locais. Novamente, assumindo que a distância entre os dois pontos é muito pequena é razoável fazer a aproximação:

Para usar essa equação, também devemos considerar que os dois pontos estão fora da zona de transição, já que as relações para são bem diferentes para cada região. Além disso, assim como especulamos no item (a), as relações para o coeficiente convectivo em placa plana, em regime laminar é e em turbulento ; então, o melhor seria aplicá-la na condição de regime turbulento, em que a influência da distância é menor.

Por fim, no item (c) devemos expressar em termos dos coeficientes médios em e . Vamos começar pensando na equação de transferência de calor por convecção, dentro do espaço :

Analogamente, podemos descrever a taxa de transferência de calor do início da placa até atingir cada ponto:

Então, o calor transferido apenas no intervalo pode ser descrito como:

Esta equação pode ser aplicada para todos os tipos de escoamento, já que depende dos valores médios dos coeficientes.