Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 103
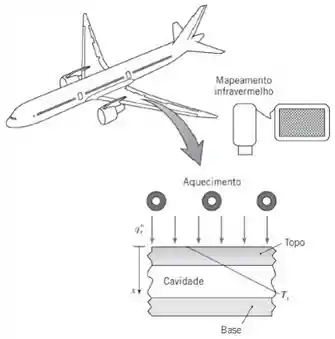
Os componentes estruturais de uma aeronave moderna são normalmente fabricados com materiais compósitos de alto desempenho. Esses materiais são fabricados pela impregnação de malhas de fibras extremamente fortes, que são moldadas em uma forma com um líquido epóxi ou termoplástico. Após o líquido curar ou resfriar, o componente resultante tem resistência extremamente alta e baixo peso. Periodicamente, esses componentes têm que ser inspecionados para garantir que as malhas de fibras e o material ligante continuem laminados e, desta forma, o componente não perca sua qualidade para uso em aeronaves. Um método de inspeção envolve a aplicação de um fluxo térmico radiante constante e uniforme na superfície sendo inspecionada. A resposta térmica da superfície é medida com um sistema de imagens em infravermelho, que captura a emissão da superfície e a converte em um mapa codificado de cores da distribuição de temperaturas na superfície. Considere o caso no qual um fluxo uniforme de é aplicado na camada externa de uma asa de avião inicialmente a . O lado oposto da camada externa, que tem de espessura, está em contato com ar estagnado, de tal forma que pode ser tratado como isolado termicamente. A massa específica e o calor específico do material da camada são e respectivamente. A condutividade térmica efetiva do material da camada intacto é Resistências de contato se desenvolvem no interior da estrutura como um resultado do esgarçamento entre as malhas de fibras e o material ligante, levando a uma condutividade térmica efetiva reduzida de Determine a temperatura da superfície do componente após e segundos de irradiação para (i) uma área na qual o material está estruturalmente intacto e (ii) uma área adjacente da asa onde ocorreu esgarçamento no interior da asa.
Passo 1
Vamos para mais uma questão? 😊 Aqui nós temos a espessura e temperatura inicial da camada externa. Além das propriedades do material quando intacto e quando laminado e o fluxo de calor na superfície imposta.
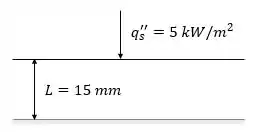
A partir dessas informações queremos encontrar a temperatura da superfície do material intacto e do material laminado, após e segundos.
Passo 2
Aqui nós vamos considerar que:
(1) A condução de calor é unidimensional;
(2) A superfície inferior é adiabática;
(3) As propriedades são constantes e uniformes;
(4) As perdas por convecção e radiação são desprezíveis.
No item (i) nós queremos a temperatura da superfície do componente para uma área na qual o material está estruturalmente intacto.
A situação é equivalente a uma parede plana de espessura com fluxo de calor em ambas as superfícies. Então, vamos utilizar a Tabela 5.2b (Casos Interiores, Parede Plana de espessura ). Primeiro calculamos para o caso intacto em:
Passo 3
Como ,
Então,
Passo 4
Em , temos:
E,
Passo 5
No item (ii) nós queremos a temperatura da superfície do componente para uma área adjacente da asa onde ocorreu esgarçamento no interior da asa.
Repetindo os cálculos para , encontramos:
Resposta
(i)
(ii)