Uma placa semitransparente é irradiada uniformemente em cima e em baixo, enquanto ar a escoa sobre as superfícies superior e inferior, fornecendo um coeficiente de transferência de calor convectivo uniforme de A absortividade da placa em relação à irradiação é de . Sob condições de regime estacionário, medidas feitas com um detector de radiação acima da superfície superior indicam uma radiosidade (que inclui transmissão, assim como reflexão e emissão) de , enquanto a placa está a uma temperatura uniforme de .
Determine a irradiação e a emissividade da placa. A placa é cinza para as condições especificadas?
Passo 1
Bora para mais uma questão?! Aqui a questão nos deu as condições de temperatura, absorção, transmissividade, radiosidade e convecção para uma placa semitransparente. Ilustrativamente nós temos:
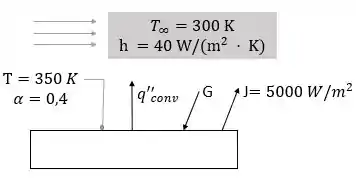
Com isso, queremos encontrar a irradiação e a emissividade da placa, show? Então vamos lá!
Passo 2
Não temos um tapete mágico, mas para resolver essa questão vamos assumir um mundo ideal onde temos as condições de estado estacionário e condições uniformes da superfície, tá bem? Rs
Do balanço de energia na placa temos:
Resolvendo para irradiação e substituindo os valores numéricos,
Passo 3
Maaas, além da irradiação também queremos encontrar a emissividade. Para isso vamos utilizar a radiosidade,
Resolvendo para emissividade e substituindo os valores numéricos,
Então,
E a superfície não é cinza para as condições dadas. Com isso concluímos mais uma questão.(uhuul!)
Resposta
A superfície não é cinza para as condições dadas.