Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 66

Um potencial de velocidade plano em coordenadas polares é definido por

ϕ = K c o s θ r ; K = c o n s t

Encontre a função corrente para esse escoamento, faça o esboço de algumas linhas de corrente e linhas equipotenciais e interprete o padrão de escoamento.

Passo 1

Bora pra mais uma!

Temos que:

V r = ∂ ϕ ∂ r = 1 r ∂ ψ ∂ θ ; V θ = 1 r ∂ ϕ ∂ θ = - ∂ ψ ∂ r

V r = - K c o s θ r 2 = 1 r ∂ ψ ∂ θ ; V θ = - K s e n θ r ² = - ∂ ψ ∂ r

Daí, podemos integrar as duas equações e compara-las para obter ψ ( r , θ ) :

∂ ψ ∂ θ = - K c o s θ r →   ψ = - K s e n θ r + C r

∂ ψ ∂ r = K s e n θ r 2 →   ψ = - K s e n θ r + c θ

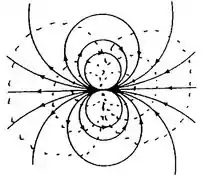
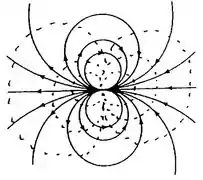
Portanto: ψ r , θ = - K s e n θ r + C . Cujo esboço é:

Resposta

A função corrente para esse escoamento é ψ r , θ = - K s e n θ r + C e as linhas de corrente deste escoamento seguem um padrão de escoamento de duplo fluxo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O escoamento potencial em torno de uma cunha com semiângulo θ conduz a uma aplicação importante da teoria de camada-limite laminar chamada de escoamentos de Falkner-Skan [ 15 ,p .239 – 245 ] . Seja x
Investigue o potencial complexo f z = A cosh ⁡ [ p ( z / a ) ] e trace as linhas de corrente dentro da região mostrada na Figura P 8.69 . Que palavra hifenizada (de origem francesa) pode descrever tal
A velocidade não viscosa ao longo da cunha do Problema P 8.65 tem uma forma analítica U x = C x m , em que m = n– 1 e n é o expoente na Equação ( 8.53 ) . Mostre que, para quaisquer C e n , o cálculo
Combine o escoamento de estagnação da Figura 8.19 b com uma fonte na origem: f z = A z 2 + m ⋅ ln ⁡ z Trace as linhas de corrente para m = A L 2 , sendo L uma escala de comprimento. Interprete.
Investigue o potencial complexo f z = U ∞ ( z + a 2 / z ) e interprete o padrão de escoamento.