Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas de Projeto - Ex. 1
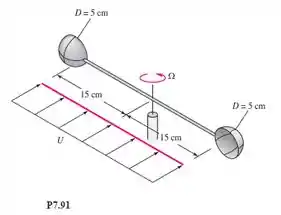
PP7.1 – Deseja-se projetar um anemômetro de concha para medir a velocidade do vento, semelhante ao da Fig. P7.91, com uma abordagem mais sofisticada que a do método do “torque médio” do Problema 7.91. O projeto deve alcançar uma relação aproximadamente linear entre velocidade do vento e velocidade de rotação, na faixa de 32
Passo 1
Vamos começar formulando as hipóteses que podem ser feitas.
Vamos lembrar que o arrasto é a perda de escoamento de um fluxo de um fluido que se atrita com um determinado corpo se está submerso neste fluido.
O arrasto é diretamente proporcional ao ângulo θ, e também diretamente proporcional a velocidade linear do escoamento do fluido, U. O ângulo em questão influenciará diretamente no padrão de escoamento do fluido que variará conforme o tempo decorre, pois o ângulo se altera com o tempo, assim, para certos valores de θ, o arrasto promoverá um escoamento do tipo laminar, enquanto para certos outros valores de θ, o arrasto fornecerá um escoamento turbulento.
Assim, com diferentes padrões de escoamento, haverá diferentes correlações para se determinar o coeficiente de arrasto e coeficiente de pressão, que tornará os cálculos mais complexos. Uma hipótese apropriada que se pode fazer é considerar o escoamento como não viscoso, simplificando assim a modelagem relacionada ao arrasto.
Passo 2
Vamos agora determinar uma expressão para o torque instantâneo, T(t).
Vamos relembrar que o torque é definido pela seguinte relação matemática:
Onde, r é raio de torção e F é a força aplicada que gera a torção.
Em um elemento diferencial, então, pela relação anterior, podemos escrever o diferencial do torque como:
Assim, o torque total será:
Onde, F para este caso é a força de arrasto que é dada pela seguinte equação:
Onde, U é a velocidade linear que é expressa em função da velocidade de rotação
Logo,
Diferenciando:
Assim,
Passo 3
Integrando a equação anterior vamos chegar que:
O coeficiente de arrasto dependerá do ângulo θ pela seguinte expressão
Onde
Assim,