Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 13

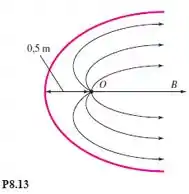
13 – Um pequeno tanque de peixes é aproximado por um formato de semicorpo, como mostra a Fig. 8.13. O ponto O, a 0,5 m de distância da borda esquerda do tanque, é uma fonte de água descarregando aproximadamente 0,35 m3/s por metro de profundidade normal ao papel. Encontre o ponto B ao longo do eixo no qual a velocidade da água é aproximadamente 25 cm/s.

Passo 1

Vamos pegar a equação que descreve o comportamento do escoamento da água descarregando no tanque com o formato da figura 8.13.

Como se trata de um semicorpo, então podemos usar a equação 8.20, cuja expressão é:

V 2 = U 2 1 + a 2 r 2 + 2 a r cos ⁡ θ

Onde, a é a distancie da borda do tanque e θ é o ângulo entre o ponto O e o ponto B.

a = 0,5   m

θ = 0 °

Passo 2

Vamos tentar isolar r, que é a distância entre o ponto O e o ponto B, que queremos encontrar

V 2 = U 2 1 + a 2 r 2 + 2 a r cos ⁡ θ

V 2 U 2 = 1 + a 2 r 2 + 2 a r cos ⁡ θ

1 r a 2 r + 2 a cos ⁡ θ = V 2 U 2 - 1

Ou,

a 2 + 2 a r cos ⁡ θ r 2 = V 2 U 2 - 1

a 2 + 2 a r cos ⁡ θ = V 2 U 2 - 1 r 2

V 2 U 2 - 1 r 2 - 2 a cos ⁡ θ r - a 2 = 0           E q 1

Passo 3

A velocidade U, você pode ser encontrar usando a informação da vazão.

Como foi dito que a vazão é a vazão volumétrica por profundidade normal, assim podemos determinar a velocidade U pela seguinte expressão:

U = Q π a

Onde, Q é a vazão que é

Q = 0,35 m 3 s m

Assim,

U = 0,35 m 3 s . m π 0,5   m = 0,22 m s = 22 c m s

Passo 4

Voltando na Eq.1

V 2 U 2 - 1 r 2 - 2 a cos ⁡ θ r - a 2 = 0

Aplicando os valores já conhecidos:

25 2 22 2 - 1 r 2 - 2 ( 0,5 ) cos ⁡ ( 0 ) r - ( 0,5 ) 2 = 0

0 , 26 r 2 - r - 0,25 = 0           E q 2

Passo 5

Resolvendo a equação do segundo dada pela Eq2:

Usando Bhaskara:

r = - b ± b 2 - 4 a c 2 a

O único valor possível para r é um valor positivo, então:

r = - b + b 2 - 4 a c 2 a

Atribuindo os valores das constates da Eq2:

r = - - 1 + - 1 2 - 4 0,26 - 0,25 2 0,26

r = 4,1   m

Então o ponto B está a cerca de 4,1 m do ponto O.

Resposta

Ponto B:

r = 4,1   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco desliza para baixo em uma parede longa, reta, inclinada, com a velocidade V , sobre um filme fino de óleo de espessura h (Figura P9-113).O peso do bloco é W ,e sua área de contato com a filme
Considere o seguinte escoamento incompressível bidimensional, que claramente satisfaz a continuidade: u = U 0 = c o n s t a n t e ,v = V 0 = c o n s t a n t e Encontre a função corrente ψ ( r , θ ) pa
Considere o potencial de velocidade incompressível bidimensional ϕ = x y + x 2 - y 2 . (a) É verdade que ∇ 2 ϕ = 0 , e, em caso afirmativo, o que isso significa? (b) Se ela existe, encontre a função c
Um campo de escoamento incompressível bidimensional é definido pelos componentes de velocidade u = 2 V x L - y Lv = - 2 V y L em que V e L são constantes. Se elas existem, encontre a função corrente e
Um líquido é drenado por um pequeno furo em um tanque, como mostra a Figura P4.60, de forma que o campo de velocidade é dado por v r ≈ 0 , v z ≈ 0 , v θ ≈ K R 2 / r , em que z = H é a profundidade da