Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas de Projeto - Ex. 1
PP10.1 – Um canal reto em terra com vegetação rasteira tem um formato trapezoidal da Fig. 10.7, com b = 4 m e θ = 35°. O canal tem uma declividade de fundo constante de 0,001. A vazão varia sazonalmente de 5 até 10 m3/s. Deseja-se instalar um vertedouro de soleira delgada através do canal de modo que a profundidade da água, 1 km a montante, permaneça a 2 m ± 10% ao longo de todo o ano. Verifique a possibilidade de fazer isso com um vertedouro de largura total; se tiver sucesso, determine a altura apropriada do vertedouro Y; caso contrário, tente outras alternativas, tais como
A) um vertedouro de soleira espessa de largura total ou;
B) um vertedouro com contrações laterais ou;
C) um vertedouro com entalhe V.
Qualquer que seja seu projeto final, cite a variação sazonal das propriedades normais e críticas para comparação com a profundidade nominal desejada de 2 m.
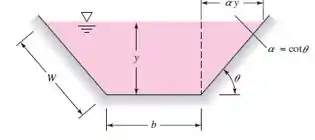
Figura 10.7
Passo 1
A ideia deste problema, é fazer uma verificação, com os dados e informações fornecidas, se é possível de se usar um vertedouro do tipo soleira delgada de largura total para ser aplicado como medidor de vazão para o escoamento de água no canal aberto caracterizado geometricamente pela fig. 10.7.
Vamos precisar de saber como fazer essa verificação se um vertedouro de soleira delgado de largura total é viável dentro das especificações estabelecidas.
Para isso, vamos determinar o valor da diferença de altura entre a profundidade de água e o topo do vertedouro, H, para as vazões de 5 e 10 m3/s.
Passo 2
Vamos relembrar que a Eq. de projeto de um vertedouro é dado pela eq. 10.55 do White, cuja expressão é:
Onde, CD é o coeficiente de descarga do vertedouro e este coeficiente é dado por:
Onde, para ser válido a equação da vazão, deve-se seguir a seguinte relação:
Considerando um valor limite para a razão H/Y, isto é, para H/Y = 2, vamos ter que:
Assim,
Passo 3
Isolando H na equação anterior, vamos ter que:
Aplicando os valores para as vazões:
-Q = 5 m3/s:
-Q = 10 m3/s:
Passo 4
Assim, como a altura H foi menor que 2 m para os dois casos, então possivelmente a profundidade de água no canal aberto para a faixa de vazão sazonal seja em torno de mais ou menos 2 m.
Para a altura Y, que promova uma profundidade de mais ou menos 2 m e que também obedeça a relação do coeficiente de descarga, podemos determina-lo da seguinte forma:
Atribuindo um valor médio para H entre os valores encontrados:
Assim, o valor de Y é:
Conferindo:
Portanto, o vertedouro de soleira delgada é apropriado para o projeto.
Resposta
O vertedouro de soleira delgada é apropriado para o projeto.