Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 141

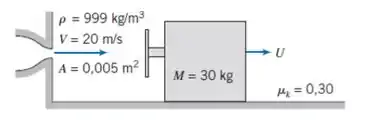
Um conjunto pá/bloco deslizante move-se sob a ação do jato de um líquido, conforme mostrado. O coeficiente de atrito cinético para o movimento do bloco ao longo da superfície é μ k = 0,30 . Calcule a velocidade terminal do bloco.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V = v - u ) ;
  4. Escoamento uniforme;

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema x , temos:

F S x + F B x - ∫ V C a r f x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não há forças de campo atuando no sistema e nem resistência superficial, então, F B x = 0 :

F S x - ∫ V C a r x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

F S x - a x m = ∫ S C u ( ρ V ) d A

Sendo que:

F S x = - m g μ k

Então:

- m g μ k - a x m = ∫ S C u ( ρ V ) d A

Passo 3

- m g μ k - a x m = ∫ S C u ( ρ V ) d A

Para o fluxo de entrada, V   e   A possuem uma inclinação de 180°, então ρ V A = ( - ρ V A ) .

- m g μ k - a x m = u 1 - ρ V A + u 2 ρ V A + u 3 ρ V A

Sendo:

u 1 = v - u ;

u 2 = 0 .

u 3 = 0 .

Então:

- m g μ k - a x m = v - u ⋅ - ρ V A + 0   ⋅   ρ V A + 0 ⋅ ρ V A

- m g μ k - a x m = v - u ⋅ v - u ⋅ - ρ A

a x = v - u 2 ⋅ ρ A m - g μ k

Passo 4

Temos que:

∫ d u d t = a x

Então:

∫ d u d t = v - u 2 ⋅ ρ A m - g μ k

Sendo:

∫ d u d t = 0

Temos:

0 = v - u 2 ⋅ ρ A m - g μ k

v - u = m g μ k ρ A

u = v - m g μ k ρ A

Passo 5

Para resolvermos a equação obtida, temos:

v = 2 0   m / s ;

m = 30   k g ;

ρ = 1000   k g / m 3 ;

g = 9,8   m / s 2 ;

μ k = 0,30 ;

A = 0,005   m 2 .

Assim:

u = 20 - 30 ⋅ 9,8 ⋅ 0,30 1000 ⋅ 0,005 =

u = 15,8   m / s  

Resposta

u = 15,8   m / s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um líquido de massa especifica ρ escoa em uma curva a 90 ° , como mostra a Figura P3.125, e sai verticalmente e uniformemente por um trecho poroso de comprimento L. Desprezando os pesos do tubo e do l
O irrigador de gramados de três braços da Figura P3.114 recebe água a 20°C pelo centro, a 2,7 m 3 / h . Se o atrito no anel central é desprezível, qual será a rotação permanente, em rpm, para (a) θ =
Uma turbomáquina simples é constituída de um disco com dois dutos internos que saem tangencialmente através de seções quadradas, como na Figura P3.117. Água a 20°C entra perpendicularmente ao disco no
No Problema P3.60, encontre o torque em torno do flange 1 se o ponto central de saída 2 está a 1,2m diretamente abaixo do centro do flange.
Um jato de água de 3 cm de diâmetro atinge uma placa normal, como na Figura FE3.5. Se a força necessária para escorar a placa é de 23 N, qual é a velocidade do jato? (a) 2,85 m/s, (b) 5,7 m/s, (c) 8,1