Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 33

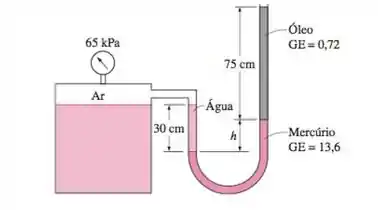
A pressão manométrica do ar no tanque mostrado é medida como 65 kPa. Determine a altura diferencial h da coluna de mercúrio.

Passo 1

Vamos tomar a densidade da água como sendo ρ á g u a = 1000   k g / m ³ .

O óleo e o mercúrio são dados seus valores de densidade específica e como sabemos a gente tem que G E i = ρ i ρ á g u a e com isso conseguimos ter os valores das densidades de cada fluido, beleza?

Passo 2

Vamos tomar o ponto da base da altura h como referência e ali, sabemos que as pressões devem ser iguais, certo?

P 1 + P á g u a = P H g + P ó l e o + P a t m

Rearranjando, vamos ter:

P 1 - P a t m = P H g + P ó l e o - P á g u a

P 1 - P a t m = P m a n o m é t r i c a = ρ ó l e o g h ó l e o + ρ H g g h H g - ρ á g u a g h á g u a

Aqui vem um pulo do gato, se liga!

Vamos dividir a equação por ρ á g u a g

P m a n o m é t r i c a ρ á g u a g = G E ó l e o h ó l e o + G E H g h H g - h á g u a

Passo 3

Perceba uma coisa antes de sair tacando os valores ali, o lado direito tem unidade de m, massssssssss o lado direito não, então vamos precisar multiplicar por um fator de conversão que eu vou deixar em destaque em negrito.

65   k P a 1000 k g m 3 9,81 m s 2 1000   k g m s 2 1   k P a . m 2 = 0,72 × 0,75 + 13,6 h H g - 0,3

h H g = 0,47   m  

Resposta

h H g = 0,47   m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um dia normal ao nível do mar, um manômetro, colocado abaixo da superfície do oceano ( d = 1,025 ) , registra uma pressão absoluta de 1,4M P a . A que profundidade se encontra o instrumento? 4m 129
Na figura FE2.3, se o óleo na região B tem d = 0,8 e a pressão absoluta no ponto B é 96,5 k P a , qual é a pressão absoluta no ponto A?
Um malandro colocou óleo, de densidade d o , no ramo esquerdo do manômetro da Figura PQ2.2. Não obstante, o tubo em U ainda é útil como um dispositivo de medida de pressão. Ele é ligado a um reservató
Alguns manômetros são construídos como na Figura PA2.1, em que um lado é um grande reservatório (diâmetro D ) e o outro lado é um pequeno tubo de diâmetro d , aberto para a atmosfera. Em um caso assim
Na figura abaixo ambas as extremidades do manômetro são abertas à atmosfera. Calcule a densidade do fluido X.