No Problema , o diâmetro do tubo é triplicado para reduzir as perdas do tubo. Determine o aumento percentual na saída de potência liquida como resultado dessa modificação.

Desprezando as perdas menores, podemos utilizar a equação de energia (que é a de Bernoulli, com alguns acréscimos). Assim, estabelecendo os pontos de análise e , temos:

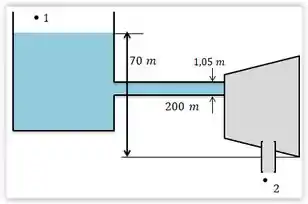
Pelo diagrama, os pontos e são expostos a atmosfera, ou seja, . Além disso, o nosso ponto de referência é em e as velocidade são praticamente desprezíveis, ou seja, . Por ultimo, não temos bomba, então . Assim, temos:

Agora, vamos aos cálculos das variáveis. Tendo duas situações, as velocidades são:

A rugosidade dos tubos sobre o diâmetro é:

Calculando o numero de Reynolds:

Com esses resultados, vamos determinar o fator de atrito através do diagrama de Moody:

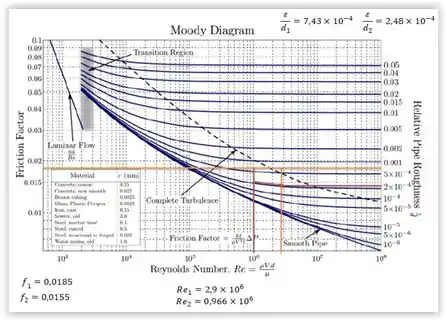
Assim, o fator de atrito é e .

Voltando a expressão que calculamos no passo , calculamos a perda de carga:

Substituindo:

Podemos calcular o aumento percentual pela razão entre a diferença perdas da turbinas e a perda antes de dobramos o diâmetro:

Prontinho!!