Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas para exames de fundamentos de engenharia - Ex. 7
Se no problema FE 6.6 o tubo é rugoso e a vazão real é de 90 m³/h, então a altura média esperada da rugosidade do tubo é de aproximadamente
- 1 mm
- 1,25 mm
- 1,5 mm
- 1,75 mm
- 2 mm
Passo 1
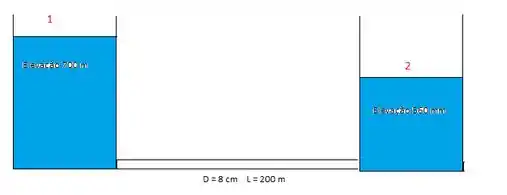
E aí, gente!! Tudo tranquilo? Vamos primeiro relembrar da física do problema citado!
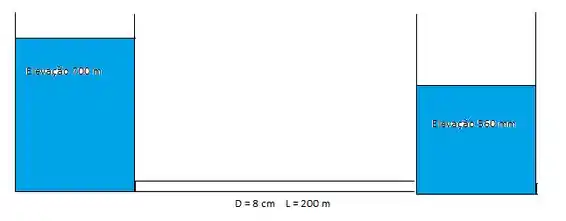
Passo 2
Bem, se eu tenho vazão eu consigo calcular a velocidade, certo?
Vamos calcular o Reynold também agora:
Passo 3
Se você lembrar da questão 6, você vai lembrar que as simplificações nos deram a seguinte equação ao final:
Opa, vamos isolar f:
Passo 4
Agora, se liga!! Bem, a gente tem os valores de Reynold e f!
Então a gente agora vai olhar no diagrama de Moody mais ou menos em qual curva de rugosidade relativa que ele estará atingindo.
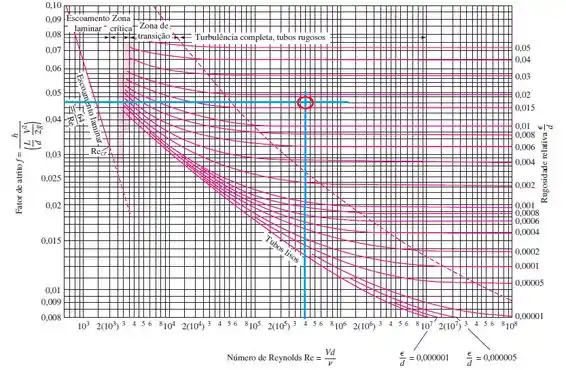
Isso dá pra gente uma rugosidade relativa em torno de 0,0175
Resposta
(e) 1,25 mm
Exercícios de Livros Relacionados
Você é chamado para especificar uma instalação de bomba de abastecimento de água do “Sears Tower” em Chicago. O sistema requer 100 gpm de água bombeada para um reservatório no topo da torre, situada 3
8.180Petróleobruto(SG=0,925eν=1,0×10−4m2/s)ébombeadoatravésdeumatubulaçãoretasobrepisoplano.Alinhaéfeitade tubosdeaçode600mm(diâmetrointerno),comespessuradeparedede12mm.Atensãoadmissívelnaparededotubo
Um bocal é conectado à uma mangueira de incêndio lisa, revestida de borracha, com 100m de comprimento e 3,5c m de diâmetro. Água de um hidrante é fornecida a 350k P a (manométrica) para uma bomba auxi
Uma bomba de água pode gerar uma diferença de pressão? p( k P a ) dada por Δ p=999-859Q ² ², em que a vazão volumétrica, Q , é dada em m ³ / s ³ . Ela alimenta um tubo de 0,5m de diâmetro, rugosidade
O sistema de tubos mostrado conduz água e é construído com tubos de ferro galvanizado. Perdas menores podem ser desprezadas. A entrada está a 400k P a (manométrica) e todas as saídas estão à pressão a