Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 72
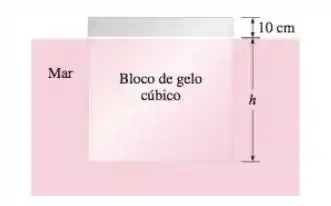
Considere um grande bloco de gelo cúbico flutuando na água do mar. As densidades do gelo e da água do mar são 0,92 e 1,025, respectivamente. Se uma parte com 10 cm de altura do bloco de gelo ficar acima da superfície da água, determine a altura do bloco de gelo abaixo da superfície.
Passo 1
Vamos começar com as hipóteses para o problema:
- A força de empuxo no ar é desprezível;
- A face superior do bloco do gelo é paralela com a superfície do mar.
Como o peso do bloco de gelo é igual a força de empuxo que está agindo sobre ele, devido ao equilíbrio estático. Assim temos que:
Passo 2
O volume é dado por , onde é a área de seção transversal do bloco de gelo. Assim,
Resolvendo para temos:
Resposta
Exercícios de Livros Relacionados
A comporta AB na Figura P2.83 é um quarto de círculo de 3 m de largura, articulada em B. Encontre a força F suficiente apenas para impedir que a comporta se abra. A comporta é uniforme e pesa 13.350 N
Determine (a) a força hidrostática total sobre a superfície curva AB da Figura P2.84 e (b) sua linha de ação. Despreze a pressão atmosférica e considere a superfície com largura unitária.
A garrafa de champanhe (d = 0,96) da Figura P2.87 está sob pressão, como mostra a leitura do manômetro de mercúrio. Calcule a força líquida sobre a extremidade hemisférica de 50 mm de raio no fundo da
Calcule os componentes horizontal e vertical da força hidrostática no painel de um quarto de círculo no fundo do tanque de água da Figura P2.85.
A comporta BC em forma de um quarto de círculo da Figura P2.86 é articulada em C. Encontre a força horizontal P necessária para manter a comporta parada. Despreze o peso da comporta.