Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 88

Um procedimento simples para a medição de coeficientes de transferência de calor por convecção em superfícies envolve o revestimento da superfície com uma fina película de um material com uma temperatura de fusão bem definida. A superfície é, então, aquecida e, pela determinação do tempo necessário para que a fusão ocorra, o coeficiente convectivo é determinado. O dispositivo experimental mostrado na figura a seguir usa esse procedimento para determinar o coeficiente convectivo em um escoamento de um gás normal a uma superfície. Especificamente, um longo bastão de cobre é embutido no interior de um material superisolante com condutividade térmica muito baixa e uma película muito fina é aplicada sobre a sua superfície exposta.

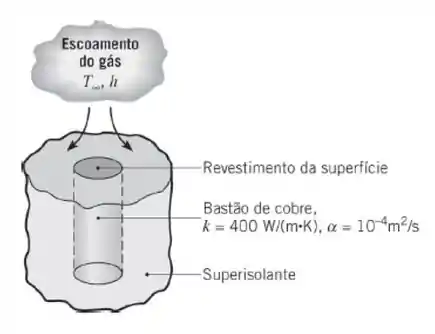
Se o bastão está inicialmente a 25 °C e o escoamento do gás, para o qual h = 200 W/(m² · K) e T ∞ = 300 °C, tem início, qual é o ponto de fusão do revestimento se a sua fusão ocorrer no instante t = 400 s?

Passo 1

Beleza! Nesse exercício, vamos modelar o problema como sendo um sólido semi-infinito com convecção na superfície, dessa forma, temos que a equação 5.63 fornece informações sobre a temperatura em um determinado ponto e instante, então, teremos:

T x , t - T i T ∞ - T i = erfc ⁡ x 2 α t - exp ⁡ h x k + h 2 α t k 2 e r f c x 2 α t + h α t k

Então, como estamos interessados no ponto de fusão se ela ocorrer no instante t = 400 s, sabemos que ela ocorrerá primeiro na superfície, então, teremos:

x = 0

t = 400   s

Então, a equação acima se torna:

T s - T i T ∞ - T i = erfc ⁡ 0 2 α t - exp ⁡ h ( 0 ) k + h 2 α t k 2 e r f c 0 2 α t + h α t k

T s - T i T ∞ - T i = 1 - exp ⁡ h 2 α t k 2 e r f c h α t k

Passo 2

Agora nós vamos substituir os valores conhecidos na equação encontrada no passo 2, dessa forma, temos:

T s - 25 300 - 25 = 1 - exp ⁡ 200 2 ( 10 - 4 ) ( 400 ) 400 2 e r f c 200 10 - 4 ( 400 ) 400

T s - 25 275 = 1 - 1,01 erfc ⁡ 0,1

Então, agora precisamos recorrer à tabela B.2 do apêndice B para encontrar o valor da função erro de Gauss, com isso, a nossa equação se torna:

T s - 25 275 = 1 - 1,01 0,888 → T s = 53,3   ° C

Resposta

T s = 53,3   ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espessa prancha de madeira ( k = 0,17W / ( m . K ) e α = 1,28 . 10 - 7 m 2 / s ) inicialmente a uma temperatura uniforme 25° C é exposta a gases quentes a 550º C º por um período de 5 minutos. O c
A temperatura do solo nas camadas superiores varia em condições atmosféricas. Antes de uma frente fria chegar, ao solo no local está a uma temperatura uniforme de 15° C . Em seguida, a área é submetid
Um bloco espesso de alumínio inicialmente a 20° C é submetido a um fluxo de calor constante de 4000W / m 2 por meio de um aquecedor de resistência elétrica cuja superfície superior é isolada. Determin
Uma pessoa descalça cujos pés estão a 32° C pisa em um bloco de alumínio a 20° C . Considerando tanto os pés quanto o bloco de alumínio como sólidos semi-infinitos, determine a temperatura da superfíc
Em áreas onde a temperatura do ar permanece abaixo de 0° C por longos períodos de tempo, o congelamento da água nas canalizações subterrâneas é uma grande preocupação. Felizmente, o solo permanece rel