Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 56
No processamento térmico de materiais semicondutores, a têmpera é efetuada pelo aquecimento de pastilhas de silício de acordo com uma programação temperatura-tempo e, a seguir, pela manutenção em uma temperatura fixa e elevada por um período de tempo preestabelecido. No dispositivo para o processamento mostrado adiante, a pastilha encontra-se em uma câmara onde há vácuo, cujas paredes são mantidas a 27°C, no interior da qual lâmpadas de aquecimento mantêm um fluxo térmico radiante na superfície superior da pastilha. A pastilha possui espessura de 0,78 mm, sua condutividade térmica é de 30 W/(m · K) e sua emissividade é igual à sua absortividade em relação ao fluxo térmico radiante (ε = = 0,65). Para = 3,0 × W/m², a temperatura em sua superfície inferior é medida por um termômetro de radiação, sendo igual a = 997°C.
Para evitar o empeno da pastilha e a indução de planos de deslizamento na estrutura do cristal, a diferença de temperaturas ao longo da espessura da pastilha deve ser inferior a 2°C. Esta condição está sendo satisfeita?
Passo 1
Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.
Segundo o enunciado, queremos encontrar a temperatura da superfície superior ( da pastilha de silício, de modo a comparar com a temperatura da superfície inferior () para saber se esta diferença é menor que 2 para evitar que a pastilha empene.
Para isso, devemos fazer um balanço de energia na superfície superior da placa. Antes, devemos assumir algumas hipóteses simplificadoras para darmos embasamento física a nossa análise. Fique de olho:
- Em primeiro lugar, vamos considerar este um processo em estado estacionário, sem acúmulo;
- Vamos considerar, também, uma transferência de calor unidimensional;
- Por fim, como está no enunciado, a pastilha encontra-se em uma câmara a vácuo, onde não há fluido e, portanto, não há transferência de calor por convecção.
Para fazermos nosso balanço, devemos prestar atenção no esquema apresentado na figura abaixo:
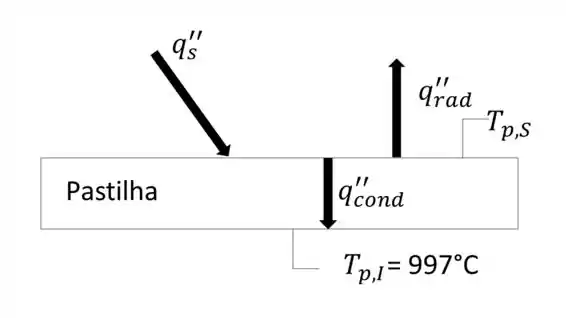
Fazendo um balanço sem acúmulo, temos que o fluxo de energia que entra é igual ao que sai do volume de controle (parede superior da pastilha):
Consideramos, então, o fluxo de energia que entra como a porção = 0,65 absorvida pela pastilha, e os fluxos de energia radiante e condutivo. O nosso balanço se torna, então:
Eu sei que nesse Passo 1 te dei muitas informações, mas antes de ir pro Passo 2, vou te mostrar algumas grandezas fornecidas pelo enunciado pra você guardar na memória:
Passo 2
Vamos agora destrinchar o balanço que eu te mostrei no passo 1. Em primeiro lugar, para calcular o fluxo radiante emitido pela superfície superior, devemos utilizar a seguinte equação:
Sendo a constante de Stefan–Boltzmann, que vale .
Além disso, quero dar uma dica: quando você for calcular uma taxa ou um fluxo de calor por radiação, lembre sempre de colocar a tempera em K, senão seu cálculo vai estar errado.
Sabendo disso, vamos deixar então o nosso fluxo radiante em função de :
Agora, vamos calcular o fluxo condutivo a partir da equação abaixo:
Substituindo no balanço do Passo 1:
Reorganizando a equação para explicitar :
Para encontrar o valor de basta resolver a equação acima. Nesta resolução, foi utilizado o método de busca direta em uma calculadora, mas você pode se sentir livre para resolver da maneira que desejar. Sendo assim:
Logo, a diferença entre as temperaturas pode ser calculada como:
Como a diferença é menor que , a pastilha não vai empenar.
Resposta
Como demonstrado no Passo 2, a diferença de temperatura é