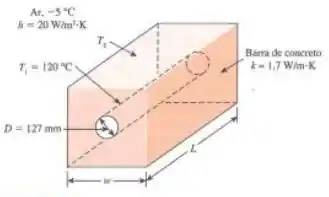
No processo de geração de calor e energia combinados (CHP), o subproduto calor é usado para aquecimento doméstico ou industrial. Vapor quente é produzido a partir da planta de cogeração por um tubo com diâmetro de 127 mm centrado na secção de barra sólida de concreto transversal quadrada, com condutividade térmica de . A temperatura da superfície do tubo é constante em 120 °C, enquanto a barra de concreto quadrada é exposta ao ar com temperatura de -5 °C e coeficiente de transferência de calor por convecção de . Se a diferença de temperatura entre a superfície externa da barra de concreto quadrada e do ar ambiente for mantida a 5 °C, determine a largura da barra de concreto e a taxa de perda de calor por metro de comprimento.

Começamos a questão deixando claro quais são as nossas hipóteses para o problema. Neste caso, temos condução de calor unidimensional e em regime permanente, propriedades térmicas constantes, é desconsiderado o efeito da radiação, a parede do tubo e o contato tubo – barra de concreto são desconsiderados.

Vamos começar a questão determinando a largura da barra de concreto. Para isto, é necessário determinar o fator de forma de acordo com a configuração do problema. Utilizando a fórmula obtida da tabela 3-7, temos:

Portanto, a taxa de transferência de calor por condução é dada por:

Contudo, como estamos em regime permanente (não há acúmulo de calor) e não há geração de calor, todo este calor é transferido para fora do bloco por convecção. Portanto, também temos a seguinte relação:

Igualando ambas as expressões com seus valores já substituídos e isolando os termos com , temos:

A equação só pode ser resolvida iterativamente. Portanto, resolvendo-a através de métodos iterativos, vamos obter o valor de , e assim respondemos a primeira parte da questão!