Processos de revestimento por pulverização de plasma são usados com frequência para fornecer proteção superficial a materiais que ficam expostos a ambientes hostis, que induzem a degradação da superfície por meio de fatores tais como desgaste mecânico, corrosão ou fadiga térmica. Revestimentos cerâmicos são usados comumente para esse propósito. Pela injeção de pó cerâmico através do bico (anodo) de um maçarico de plasma, as partículas são arrastadas pelo jato de plasma, no interior do qual elas são aceleradas e aquecidas.
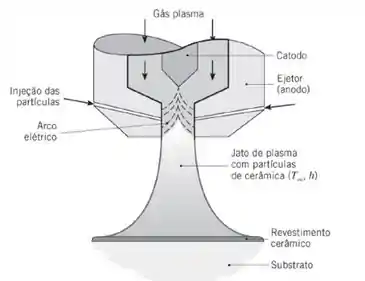
Durante o seu tempo de voo, as partículas cerâmicas devem ser aquecidas até o seu ponto de fusão e convertidas completamente para o estado líquido. O revestimento é formado com a colisão das gotas fundidas (que se espalham) sobre o material do substrato, que passam por uma rápida solidificação. Considere condições nas quais partículas esféricas de alumina (Al2O3), com diâmetro , massa específica , condutividade térmica e calor específico são injetadas no interior de um arco de plasma, que se encontra a e fornece um coeficiente para o aquecimento convectivo das partículas. O ponto de fusão e o calor latente de fusão da alumina sãoe, respectivamente.
(a) Desprezando a radiação, obtenha uma expressão para o tempo de voo, , necessário para aquecer a partícula da sua temperatura inicial até o seu ponto de fusão , e, uma vez na temperatura de fusão, para que a partícula se funda completamente. Calcule para e as condições de aquecimento especificadas.
(b) Supondo que a alumina apresente uma emissividade de e que as partículas troquem calor por radiação com uma grande vizinhança a , avalie a validade de se desprezar a radiação.
Passo 1
(a) O processo de dois passos envolve (i) o tempo t1 para aquecer a partícula até o seu ponto de fusão e (ii) o tempo t2 necessário para atingir a fusão completa. Portanto, ti-f = t1 + t2, onde de Eq. (5,5),
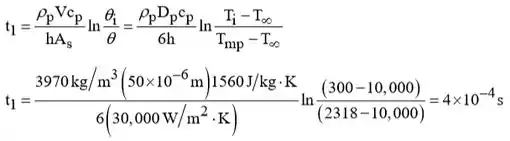
Realizando um balanço energético para o segundo passo, obtemos,
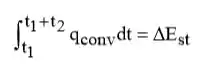
Portanto,
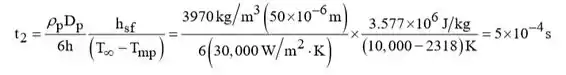
Logo,
![]()
Passo 2
(b) Contrastando o menor valor do fluxo de calor de convecção,
![]()
para o maior fluxo de radiação,
![]()
Com
![]()
Portanto, concluímos que a radiação é insignificante.