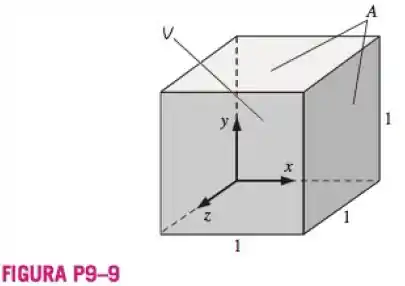
Seja o vetor ser dado por e seja o volume de um cubo de aresta unitária com seu vértice na origem, limitado por a 1, a 1 e a 1 (Fig. P9–9). A área é a área da superfície do cubo. Execute as duas integrais do teorema do divergente e verifique se elas são iguais. Mostre todo o seu trabalho.

O Teorema do Divergente é dado por:

Precisamos provar que elas são iguais, certo?

Então vamos começar pela integral do volume, à esquerda:

Substituindo

Resolvendo separadamente:

Colocando na segunda integral:

Agora nós vamos resolver esta segunda integral:

Agora colocamos o resultado dentro da terceira integral:

Agora vamos olhar para a segunda integral do Teorema do Divergente:

Para achar os vetores para as seis fases do cubo vamos lançar mão de um desenho:

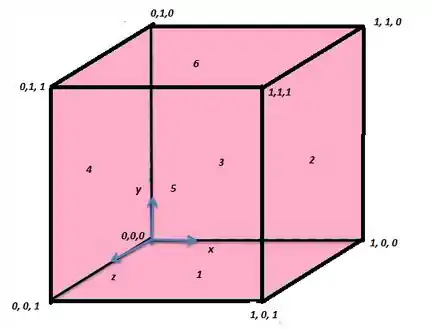
Então, o vetor unitário será:

Agora que já temos o vetor unitário para lado vamos aplicar no termo .

Lado 1:

Como o lado 1 é caracterizado por apresentar

Lado 2:

Como o lado 2 é caracterizado por apresentar

Lado 3:

Como o lado 3 é caracterizado por apresentar

Lado 4:

Como o lado 4 é caracterizado por apresentar

Lado 5:

Como o lado 5 é caracterizado por apresentar

Lado 6:

Como o lado 6 é caracterizado por apresentar

Agora vamos olhar como ficaria estes dados na nossa integral de superfície:

Já vou logo zerando as que deram zero:

Substituindo nossos valores nas integrais prestando bastante atenção aos limites que vimos na figura:

Resolvendo as primeiras integrais e aplicando os intervalos:

Portanto:

Sendo assim:

Ufaaa !! Puxado, não foi?