Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 8

For the velocity distribution u 5 2By, υ 5 1Bx, w 5 0,

evaluate the circulation Γ about the rectangular closed

curve defined by (x, y) 5 (1,1), (3,1), (3,2), and (1,2). Interpret your result, especially vis-ã -vis the velocity potential.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

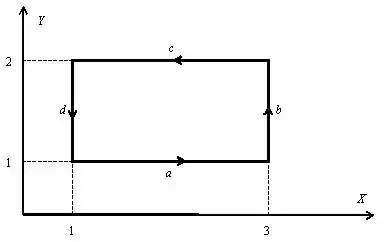
Desenhe a curva de fechamento com as coordenadas dadas, conforme mostrado:

Passo 2

A circulação ao redor da curva é a soma de a , b , c , d e dada por,

Γ   = ∫ c     V ⋅ d s   = ∫ a     u d x + ∫ b     v d y + ∫ c     u d x + ∫ d     v d y

Substitua - B y para u , B x para v , e 0 para w .

Γ   = ∫ a     ( - B y ) d x + ∫ b     ( B x ) d y + ∫ c     ( - B y ) d x + ∫ d     ( B x ) d y   = ∫ a     ( - B ) y d x + ∫ b     ( B ) x d y + ∫ c     ( - B ) y d x + ∫ d     ( B ) x d y

Substitua os valores considerando a curva de coordenadas.

Γ   = ( - B ) ( 1 ) ( 3 - 1 ) + ( B ) ( 3 ) ( 2 - 1 ) + ( - B × 2 ) ( 1 - 3 ) + ( B × 1 ) ( 1 - 2 )   = - 2 B + 3 B + 4 B - B   = 4 B

Portanto, a circulação em torno da curva fechada retangular é 4 B .

Passo 3

Verifique se o fluxo é rotacional ou irrotacional. Para um fluxo irrotacional,

2 ω z = 0

Encontre 2 ω z fazendo:

2 ω z = 2 ( ∇ × V )

Aqui, é ∇ × V a vorticidade e é dada por,

∇ × V   = i ∂ ∂ x + j ∂ ∂ y × ( u i + v j ) 2 ω z   = 2 i ∂ ∂ x + j ∂ ∂ y × ( u i + v j )   = 2 k ∂ v ∂ x - ∂ u ∂ y

Substitua - B y para u e B x para v .

2 ω z   = 2 k ∂ ( B x ) ∂ x - ∂ ( - B y ) ∂ y   = 2 k ∂ B x ∂ x + ∂ B y ∂ y   = 4 B k

Uma vez que 2 ω z ≠ 0 , o fluxo é rotacional. A magnitude da circulação é 4 B e o fluxo é rotacional.

Resposta

A magnitude da circulação é 4 B e o fluxo é rotacional.

Exercícios de Livros Relacionados

Use o modelo de escoamento potencial para aproximar o escoamento do ar de sucção de um aspirador de pó através de um adaptador com fenda bidimensional, como na figura abaixo. No plano xy através da li
Investigue o potencial complexo f z = U ∞ z + m ln ⁡ [ ( z + a ) / ( z - a ) ] e interprete o padrão de escoamento.
Mostre que o potencial complexo f = U ∞ { z + 1 4 a coth ⁡ [ π ( z / a ) ] } representa o escoamento em torno de uma oval localizada a meio caminho entre duas paredes paralelas y ± 1 2 a . Qual seria
A superposição do Problema 8.62 leva ao escoamento de estagnação próximo de uma saliência curva, em contraste com a parede plana da Figura 8.19 b . Determine a altura máxima H da saliência em função d
Trace as linhas de corrente da Equação ( 8.53 ) no quadrante superior direito para n = 4 . Como a velocidade aumenta com x ao longo do eixo x a partir da origem? Para que ângulo do canto e valor de n