O Professor D. dos Fluidos, montado em um carrossel com seu filho, levou consigo seu manômetro de tubo em U. (Você nunca sabe quando um manômetro pode ser útil.) Como mostra a Figura , o carrossel gira a uma velocidade angular constante e os ramos do manômetro estão separados . O centro do manômetro está a do eixo de rotação. Determine a diferença de altura de dois modos: (a) aproximadamente, considerando a translação do corpo rígido com a igual à aceleração média do manômetro e (b) exatamente, usando a teoria da rotação de corpo rígido. Até que ponto a aproximação é boa?

Passo 1
Bora resolver essa, antes disso vamos montar um esquema, para os tubos do monômetro.
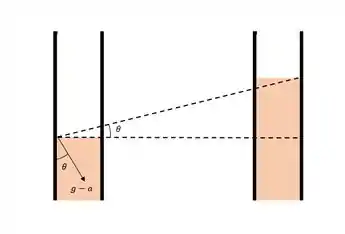
a)
A aceleração média do monômetro é dada por:
Agora encontrando a tangente do nosso ângulo :
Agora encontrando nossa altura
Passo 2
b)
Vamos considerar que o manômetro é uma parábola.
Sabemos como calcular a altura de um ponto em uma parábola, certo? Assim temos que:
Onde
Considerando de cada perna do monômetro, temos:
As repostas são praticamente iguais tendo em vista que:
Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta
a)
b)
As repostas são praticamente iguais tendo em vista que: