Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 10

Considere a geometria da bomba centrífuga idealizada descrita no Problema 10.11. Desenhe os diagramas de velocidades de entrada e de saída supondo b = c o n s t a n t e . Calcule os ângulos de entrada das pás requeridos para entrada “sem choque” na vazão de projeto. Avalie a potência teórica de entrada na bomba na vazão de projeto.

Passo 1

Diagrama de velocidades para a entrada:

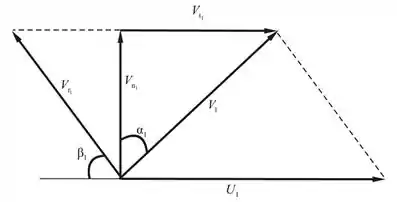
Diagrama de velocidades para a saída:

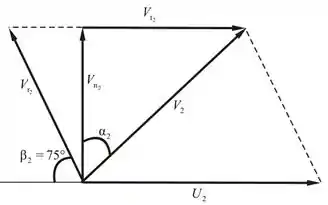
Passo 2

Encontrando a velocidade angular ω :

ω = 2 π N 60

Sendo N a velocidade de 1800   r p m :

ω = 2 π ⋅ 1800 60 = 188,5   r a d / s

Agora, calcularemos as velocidades horizontais de entrada ( U 1 ) e saída ( U 2 ) :

U = R ω

Sendo:

R 1 = 2,5   c m = 0,025   m ;

R 2 = 18   c m = 0,18   m ;

ω = 188,5   r a d / s .

Temos:

U 1 = 0,025 ⋅ 188,5 = 4,71   m / s

U 2 = 0,18 ⋅ 188,5 = 33,93   m / s

Passo 3

Calculando a componente normal V n 2 da velocidade absoluta V 2 na saída:

Q = 2 π R 2 b 2 V n 2

V n 2 = Q 2 π R 2 b 2

Sendo:

Q = 30 m 3 m i n = 0,5   m 3 / s ;

R 2 = 18   c m = 0,18   m ;

b 2 = 1   c m = 0,01   m .

Temos:

V n 2 = 0,5 2 π ⋅ 0,18 ⋅ 0,01 = 44,21   m / s

Relacionando V n 2 com os raios, conseguimos obter V n 1 da velocidade absoluta V 1 na entrada:

V n 1 = R 2 R 1 V n 2

V n 1 = 0,18 0,025 ⋅ 44,21 = 318,31   m / s

Calculando o ângulo β 1 :

β 1 = tan - 1 ⁡ V n 1 U 1 = tan - 1 ⁡ 318,31 4,71 = 89,15 °

Passo 4

Obtendo V t 1 , componente tangencial da velocidade absoluta V 1 :

V t 1 = U 1 - V n 1 cos ⁡ ( β 1 )

V t 1 = 4,71 - 318,31 cos ⁡ 89,15 ° = - 0,012   m / s

Obtendo V t 2 , componente tangencial da velocidade absoluta V 2 :

V t 2 = U 2 - V n 2 cos ⁡ ( β 2 )

V t 2 = 33,93 - 44,21 cos ⁡ 75 ° = 22,488   m / s

Calculando a vazão mássica:

m ˙ = ρ Q

Sendo:

ρ = 1000   k g / m 3 ;

Temos:

m ˙ = 1000 ⋅ 0,5 = 500   k g / s

Passo 5

Avaliando a potência teórica de entrada na bomba na vazão de projeto.

Temos uma eficiência ideal de 100 % .

Calcularemos a potência utilizando a equação de turbina de Euler:

W e n t r a d a = ( U 2 V t 2 - U 1 V t 1 ) m ˙

Substituindo os dados apresentados anteriormente:

W e n t r a d a = 33,93 ⋅ 22,488 - 4,71 ⋅ - 0,012 ⋅ 500 = 381,54   k W

Resposta

β 1 = 89,15 °

W e n t r a d a = 381,54   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Equações para o empuxo, potência e eficiência de dispositivos de propulsão foram deduzidas na seção 10.6. Mostre que aquelas equações podem ser combinadas para a condição de empuxo constante para obte
A turbina para um novo motor a jato foi projetado para condições de entrada de 1100 kPa e 925°C, recebendo 250 Kg/s a velocidade de 500 rpm e condições de saída de 550 kPa e 730°C. Se a altitude e o c
A eficiência de propulsão, η , de uma hélice é definida como a razão entre o trabalho útil produzido e a energia mecânica cedida ao fluido. Determine a eficiência de propulsão do barco em movimento do
Um modelo de um moinho de vento de pás múltiplas, típico de fazenda americana, deve ser construído para demonstração. O modelo, com D = 1m , deve desenvolver potência máxima a uma velocidade do vento
Um moinho típico de fazenda americana, com pás múltiplas, tem D = 2,1m e foi projetado para produzir potência máxima em ventos com V = 24k m / h . Estime a vazão de água fornecida como função da altur