No projeto de edifícios, a necessidade de conservação de energia exige que a área da superfície externa, As, seja minimizada. Essa exigência implica que, para uma dada área de piso desejada, devem existir valores ótimos associados ao número de andares e às dimensões horizontais do prédio. Considere um projeto no qual a área total de piso, Api, e a distância vertical entre andares, Ha, são especificadas.

(a) Se o prédio possui uma área de seção transversal quadrada com W de lado, obtenha uma expressão para o valor de W que iria minimizar a perda de calor para a vizinhança. Suponha que a perda de calor possa ocorrer nas quatro paredes laterais verticais e no teto plano. Expresse o seu resultado em termos de Api e Ha.

(b) Se Api = 32.768 m2 e Ha = 4 m, para quais valores de W e Na (número de andares) a perda de calor é minimizada? Se o valor médio do coeficiente global de transferência de calor é igual a U = 1 W/(m2 ·K) e a diferença entre as temperaturas no interior do prédio e no ar ambiente é de 25°C, qual é a perda de calor correspondente? Qual a porcentagem de redução na perda de calor em comparação com um prédio com Na = 2?

Para resolver a letra (a), devemos encontrar uma expressão para a área superficial e minimizá-la, pois assim estaremos minimizando a transferência de calor para o ambiente externo.

Vamos considerar o esquema ilustrativo do prédio:

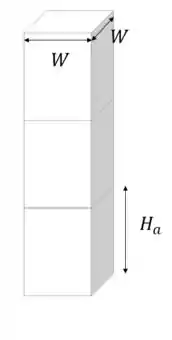
Podemos observar que cada andar possui uma altura e um piso de base quadrada de lado . Nossa área superficial, então, será uma soma da área dos quatro lados do prédio mais a área do topo:

Sendo a altura total do prédio.

Essa altura pode ser expressa como um produto do número de andares e a altura de cada andar , e nossa expressão para a área superficial se torna:

Mas o item (a) pede que a gente expresse nosso resultado em termos de e , sendo este último uma espécie de soma das áreas do piso de base quadrada de cada andar.

Ou seja, podemos expressar como um produto do número de andares pela área do pisode cada andar de passe quadrada , da seguinte forma:

Dessa forma, podemos expressar o número de andares em função de :

Podemos, então, finalmente expressar a nossa área superficial em função da área total de piso :

Mas o item não termina aí! Lembre que ele pede que a gente encontre o valor de W que minimiza a área.

Você, como um bom estudante de Engenharia, já sabe o que isso significa, né? Quando queremos minimizar ou maximizar algo, basta que a gente derive e iguale a derivada a zero. Vamo então derivar com relação a :

Igualando a derivada a zero: