Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 127
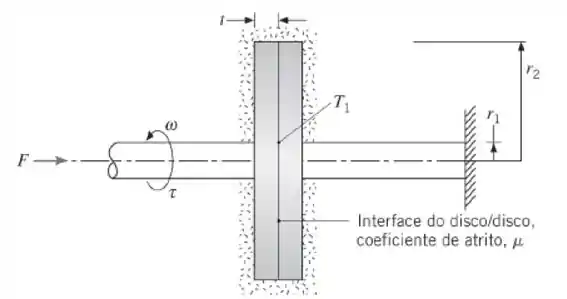
Em um teste para determinar o coeficiente de atrito μ associado a um disco de freio, um disco e o seu eixo giram a uma velocidade angular constante v, enquanto um conjunto equivalente disco/eixo permanece parado. Os discos possuem raio externo , raio do eixo , espessura e condutividade térmica . Uma força conhecida F é aplicada no sistema e o torque correspondente τ necessário para manter a rotação é medido. A pressão de contato disco/disco pode ser considerada uniforme (ou seja, independente da localização na interface) e os discos supostos termicamente isolados da vizinhança.
- Obtenha uma expressão que permita avaliar μ a partir das grandezas conhecidas.
- Para a região , determine a distribuição de temperaturas radial, T(r), no disco. Nesta distribuição, T() = é considerada conhecida.
- Sejam condições de teste nas quais . Calcule o coeficiente de atrito e a temperatura máxima no disco.
Passo 1
Vamos que vamooos !!!
Preparados??
Nós temos um eixo girando, certo? Quando isso acontece ocorre atrito ali entre eles e, como sabendo, o atrito vai produzir calor que será transmitido através do disco e não nos esqueçamos que entre os discos também vai existir atrito!
Isso nos dá a seguinte situação:
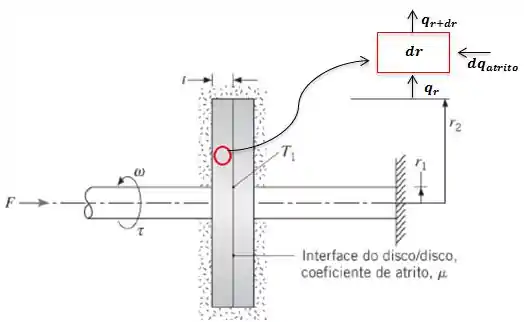
Mais tarde nós vamos precisar do balanço de energia, mas por hora vamos nos concentrar na força tangencial ao disco.
E como calculamos?
Simples:
Como estamos trabalhando com um volume diferencial:
A força é dada por:
Derivando:
Substituindo na força tangencial:
Se temos a variação da força tangencial nós podemos achar a variação do torque:
Substituindo novamente:
Se nós integrarmos esta equação para o disco inteiro:
Lembrando que:
Então:
Agora é só isolar o atrito:
E é isso aí !! Achamos o atrito em função do que nós conhecemos !!
Passo 2
Chegou a hora de fazer o balanço energético do nosso problema, certo?
Olhando na figura lá do Passo 1:
Precisamos agora calcular cada um dos termos, netão bora começar !!
Se a área é dada por:
Então:
A próxima será:
A última que nós precisamos achar é a variação da transferência de calor devido ao atrito:
Substituindo :
Agora nós substituímos tudo isso no balanço:
Substituindo
Vamos integrar uma vez, ok?
Derivamos mais uma vez:
Acabou?
Que nada !! Precisamos das condições de contorno !!
Quando não vai haver variação da temperatura com o raio, ou seja, Substituindo:
A segunda condição de contorno é que quando e :
Substituindo
Isolando
Colocando nossas constantes na fórmula da temperatura:
Agoora sim, acabamos a letra (b) !!
Passo 3
Na letra (c) nós queremos calcular o coeficiente de atrito e a temperatura máxima no disco, certo?
O problema nos disse que:
Calculando o coeficiente de atrito usando a fórmula do Passo 1:
Sabendo que a temperatura máxima ocorre quando e colocando na fórmula do Passo 2:
Substituindo nossos dados:
E é só isso galerinha !! Curtiram?
Resposta
- ;