Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 162

A transferência de calor em um transistor pode ser aumentada com a sua inserção em uma luva de alumínio ( k   =   200   W / ( m   ·   K ) ) que possui 12 aletas longitudinais usinadas sobre a sua superfície externa. O raio e a altura do transistor são r 1   =   2,5   m m e H   =   4   m m , respectivamente, enquanto as aletas possuem comprimento L   =   r 3   =   r 2   –   8   m m e espessura uniforme t   =   0,8   m m . A espessura da base da luva é r 2   –   r 1   =   1   m m e a resistência de contato na interface luva-transistor é igual a R t , c ' ' =   0,6   ×   10 - 3     m 2 ·   K / W . Ar, a T ∞   =   20 ° C , escoa sobre a superfície das aletas, fornecendo um coeficiente de transferência de calor por convecção, aproximadamente uniforme, de h   =   30   W / ( m 2   ·   K ) .

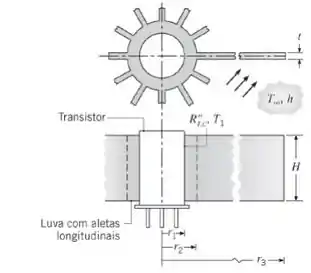
(a) Quando a superfície externa do transistor está a 80 ° C , qual é a taxa de transferência de calor através da luva?

(b) Identifique todas as medidas que podem ser tomadas para melhorar o projeto e/ou as condições operacionais, de modo que a dissipação de calor possa ser aumentada mantendo-se a temperatura externa do transistor em 80 ° C . Com palavras, avalie o mérito relativo de cada medida. Escolha, na sua opinião, as três medidas mais promissoras e numericamente avalie o efeito no desempenho térmico das mudanças correspondentes no projeto e/ou nas condições operacionais.

Passo 1

Vamos para mais uma questão 😊. Aqui nós temos as dimensões da luva de alumínio aletada inserida sobre um transistor, a resistência de contato entre luva e transistor e as condições de convecção da superfície e temperatura da caixa do transistor.

A partir disso queremos encontrar a taxa de transferência de calor da manga e as medidas para aumentar a dissipação de calor.

Passo 2

Para resolver essa questão vamos assumir que:

(1) Estamos em condição de estado estacionário;

(2) As propriedades são constantes;

(3) A transferência de calor das superfícies superior e inferior do transistor é desprezível;

(4) A radiação é desprezível;

(5) A condução radial é unidimensional.

O circuito deve levar em consideração a resistência de contato, condução na luva, convecção a partir da base exposta e condução / convecção a partir das aletas. Então, ficamos com:

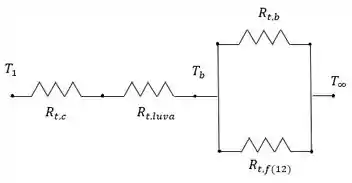
As resistências térmicas para a junta e a luva de contato são:

R t . c = R t , c ' ' 2 π r 1 H = 0,6 × 10 - 3     m 2 . K W 2 π × 0,0025 m × 0,004 m = 9,55 K W

R t , l u v a = ln ⁡ r 2 r 1 2 π k H = ln ⁡ 3,5 2,5 2 π 20 0 W m   ·   K ( 0,004 m ) = 0,0669 K W

Passo 3

Para uma única aleta, R t ,   f   = θ b q f , onde a partir da Tabela 3.4, com a convecção da ponta, temos:

q f = h P k A c 1 2 θ b sinh ⁡ m L + h m k cosh ⁡ m L cosh ⁡ m L + h m k sinh ⁡ m L

Com,

P = 2 H + t = 9,6 m m = 0,0096 m

E,

A c = t × H = 3,2 × 10 - 6 m 2

m = h P k A c 1 2 = 30 W m 2 . K × 0,0096 m 2 00 W m . K × 3,2 × 10 - 6 m 2 1 2 = 21 , 2 m - 1

m L = 21,2 m - 1 × 0,008 m = 0,170

h m k = 30 W m 2 . K 21,2 m - 1 × 200 W m . K = 0,00707

E,

h P k A c 1 2 = 30 W m 2 . K × 0,0096 m × 200 W m . K × 3,2 × 10 - 6 m 2 1 2

Passo 4

Utilizando os rendimentos da Tabela B.1, para uma única aleta temos:

R t , f = 1,014 + 0,00707 × 0,171 0,0136 W K ( 0,171 + 0,00707 × 1,014 ) = 421   K / W

Então, para 12 aletas:

R t , f ( 12 ) = R t , f 12 = 35,1   K / W

Para a base exposta, temos:

R t , b = 1 h 2 π r 2 - 12 t H = 673   K / W

Com,

R t , o = 35,1 - 1 + 673 - 1 - 1 = 33,3   K / W

Então,

R t o t = 9,55 + 0,0669 + 33,3 K / W   = 43,0   K / W

E,

q t = T 1 - T ∞ R t o t = 80 - 20 ° C 43,0   K / W = 1,40   W

Então, conseguimos resolver a letra (a), agora vamos para a letra (b) \o/

Passo 5

Com 2 π r 2   =   0,022   m e N t   =   0,0096   m , a folga existente entre as aletas é extremamente pequena ( 0,96   m m ) . Portanto, aumentando N e/ou t , seria ainda mais difícil manter um fluxo de ar satisfatório entre as aletas, e essa opção não é particularmente atraente.

Porque a eficiência da aleta para as condições prescritas é próxima da unidade ( η f = h A f R t , f - 1 =   0,992 ) , há pouca vantagem em substituir o alumínio por um material de maior condutividade térmica. Entretanto, o grande valor de η f sugere que benefícios significativos podem ser obtidos com o aumento do comprimento da aleta.

A resistência ao contato térmico é grande e, na Tabela 3.2, percebe-se que uma redução significativa pode ser efetuada usando uma folha de índio ou uma graxa condutora na zona de contato. Especificamente, é possível uma redução de R t , c ' '   de 0,6 × 10 - 3 para 10 - 4 ou 10 - 5   m 2 . K   /   W . Aumentando a velocidade do ar que flui sobre as aletas, um coeficiente de convecção maior pode ser alcançado.

Para tirar proveito de uma redução em R t , c ' '   a 10 - 5   m 2 . K   /   W , uma redução adicional em R t ,   o deve ser feita. Isso pode ser alcançado aumentando h , e para L   =   20   m m e h   =   100   W / m ^ 2   . K , R t ,   o   =   5,0   K   /   W . Com R t ,   c   =   10 - 5   m 2 K   /   W , um valor de   q t   =   11,5   W pode ser alcançado.

Resposta

  1. q t = 1,40   W
  2. Com 2 π r 2   =   0,022   m e N t   =   0,0096   m , a folga existente entre as aletas é extremamente pequena ( 0,96   m m ) . Portanto, aumentando N e/ou t , seria ainda mais difícil manter um fluxo de ar satisfatório entre as aletas, e essa opção não é particularmente atraente.

Para tirar proveito de uma redução em R t , c ' '   a 10 - 5   m 2 . K   /   W , uma redução adicional em R t ,   o deve ser feita. Isso pode ser alcançado aumentando h , e para L   =   20   m m e h   =   100   W / m ^ 2   . K , R t ,   o   =   5,0   K   /   W . Com R t ,   c   =   10 - 5   m 2 K   /   W , um valor de   q t   =   11,5   W pode ser alcançado.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma aleta cilíndrica de 0,6c m de diâmetro e 3c m de comprimento, sem grande perda de calor a partir da ponta, tem eficiência de 0,7 . A eficácia dessa aleta é a) 0,3 b) 0,7 c) 2 d) 8 e) 14
Sejam as condições do Problema 3.149, porém agora com uma espessura da parede do tubo de 5m m (diâmetros interno e externo de 50 e 60m m , respectivamente), uma resistência térmica de contato entre as
Um aquecedor de ar é constituído por um tubo de aço ( k=20W / ( m·K ) ) , com raios interno e externo r 1=13m m e r 2=16m m , respectivamente, e oito aletas longitudinais usinadas no tubo, cada uma co
Seja o cilindro de combustão com resfriamento a ar do Problema 3.160, porém em vez de impor um fluxo térmico uniforme na superfície interna, considere condições nas quais a temperatura média temporal