Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 82
O protótipo de um navio tem 122 m de comprimento e 2.787 m² de área molhada. Um modelo na escala 1:80 é testado em um tanque de reboque de acordo com a escala de Froude, com velocidades de 1,3, 2,0 e 2,7 kn (1 kn = 0,515 m/s). O arrasto de atrito medido no modelo a essas velocidades é de 0,49, 1,07 e 1,82 N, respectivamente. Quais são as três velocidades do protótipo? Qual é o arrasto de atrito estimado para o protótipo a essas velocidades, se o corrigirmos para a discrepância do número de Reynolds por extrapolação?
Passo 1
Bora pra mais uma!
Para a água a temos . Convertendo as velocidades para m/s, temos:
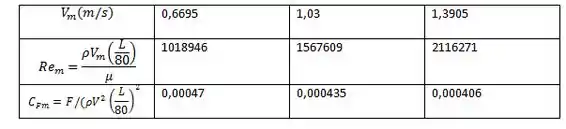
Obtemos então uma Lei de Potência expressa por:
De acordo com a escala de Froude:
Calculemos então os números de Reynolds para o protótipo:
Da lei de potência podemos estimar o coeficiente de arrasto do protótipo
1
Por fim, podemos isolar a Força e estima-la:
Resposta
As três velocidades são :
Os arrasto de atrito estimado para estas velocidades é:
