Um recipiente grande de ferro fundido ( e ) com paredes de de espessura, inicialmente a uma temperatura uniforme , está cheio com gelo a . Agora, a superfície externa do recipiente é exposta à água quente a , com um coeficiente de transferência de calor muito grande. Determine o tempo necessário para o gelo no interior do recipiente começar a derreter. Além disso, considerando o coeficiente de transferência de calor na superfície interna do recipiente como , determine a taxa de transferência de calor para o gelo através da seção de uma parede de de largura e de altura quando as condições operacionais permanentes forem atingidas. Considere que o gelo começa a derreter quando a temperatura da superfície interna sobe para .

Agora vamos para a análise do problema, pessoal! A gente pode notar que essa questão possui duas partes, sendo elas:

1. Determinar o tempo necessário para o gelo no interior do recipiente começar a derreter.
2. Determinar a taxa de transferência de calor para o gelo através da seção de uma parede de de largura e de altura quando as condições operacionais permanentes forem atingidas.

Agora que sabemos com clareza o que nos foi pedido, vamos partir para os cálculos!

Vamos começar resolvendo a parte 1 da questão, venham comigo! Como observado no enunciado, este é um problema de condução transiente em meio semi-infinito com uma temperatura superficial especificada constante. Portanto, a distribuição de temperatura em regime transiente unidimensional nesse caso é dada por:

Ainda no enunciado, nos foi dito que as paredes possuem de espessura e que inicialmente elas estavam a uma temperatura uniforme de . Agora repare na sacada! Foi pedido para considerar que o gelo começa a derreter quando a temperatura da superfície interna sobe para , portanto a temperatura tem uma variação de ! Agora que deciframos o enunciado, vamos aplicar a equação da distribuição de temperatura:

Da tabela 4-4 a gente descobre que para temos que:

Portanto, elevando os dois lados ao quadrado, temos que o tempo necessário para o gelo no interior do recipiente começar a derreter é:

Conseguimos a primeira resposta! Muito bem, vocês são feras demais!

Agora vamos para a parte 2 da questão, galera! Vem comigo que falta pouco! Precisamos determinar a taxa de transferência de calor para o gelo através da seção de uma parede de de largura e de altura quando as condições operacionais permanentes forem atingidas. Resumindo todo esse texto cansativo, queremos a taxa de transferência de calor para o gelo através da seção de área .

Como não há geração de energia interna dentro do recipiente, podemos determinar essa taxa aplicando o conceito de rede de resistência térmica! Vou fazer um esquema para facilitar a visualização: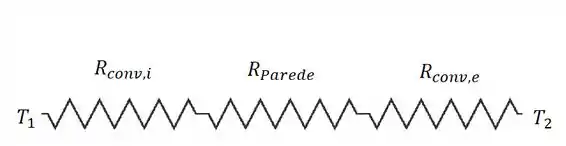

Bom, no esquema temos as temperaturas no interior do recipiente e no exterior . Além disso, temos as 3 resistências presentes na questão, sendo elas, respectivamente, a resistência térmica convectiva interna e externa ao recipiente e da , e a resistência térmica condutiva da parede onde .

Falta pouco, galera! Sabemos que a resistência térmica total pode ser calculada por:

Sabendo do enunciado que o coeficiente de transferência de calor na superfície interna do recipiente é e que o coeficiente de transferência de calor externo é muito grande, ou seja, , temos que a resistência térmica total é:

Portanto, sabendo que a taxa de transferência de calor pode ser calculada pela equação abaixo, chegamos, finalmente, no resultado final!