Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 68
68 – Um contêiner esférico de raio interno , raio externo e condutividade térmica é preenchido com água fria a . C contêiner ganha calor por convecção do ar redor a uma temperatura , com coeficiente de transferência de calor . Considerando que a temperatura da superfície interna do contêiner é de , (a) expresse a equação diferencial e as condições de contorno para a condução de calor unidimensional permanente através do contêiner, (b) obtenha a relação para a variação da temperatura do contêiner resolvendo a equação diferencial e (c) avalie a taxa de ganho de calor da água fria.
Passo 1
Desenhe a configuração do sistema fornecido.
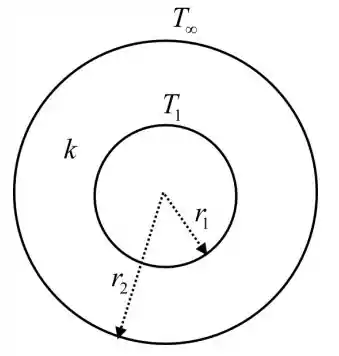
Passo 2
Escreva a equação de condução de calor para o estado estacionário unidimensional, sem geração interna de calor para coordenadas esféricas.
Aplique a primeira condição de limite.
Como o sistema é estável, o fluxo de calor conduzido para a superfície externa do recipiente é igual à transferência do fluxo de calor por convecção da superfície externa para o ambiente.
Aqui, é o fluxo de calor de condução, é o fluxo de calor convectivo.
Substitua por e por .
Aqui, a condutividade térmica do recipiente é k , o coeficiente de transferência de calor é , a temperatura do ar circundante é e é a temperatura da superfície do recipiente no raio .
Aplique a segunda condição de limite.
A temperatura na superfície interna do recipiente é zero.
Passo 3
b)
Considere a equação geral de condução de calor para o estado estacionário unidimensional, sem geração interna de calor,
Aqui é a constante de integração.
Reorganizando a expressão, temos:
Integre a equação acima para obter o perfil de temperatura.
Aqui e são constantes de integração.
Vamos encontrar os valores das constantes por meio das condições de contorno.
No raio
No raio
Passo 4
Como,
Substitua por e
Substitua o valor de da equação (1) na equação (3).
Reorganize a expressão para obter o valor de .
Vamos encontrar o valor da na equação (1).
Para isso substitua por .
Passo 5
Substitua e na equação da distribuição de temperatura,
Substituindo pelos valores conhecidos, temos:
Portanto, a variação de temperatura no recipiente é
Passo 6
c) Encontre a taxa de condução de calor na superfície do recipiente usando a equação.
Aqui, a área de seção transversal do contêiner é , é o calor perdido na superfície do contêiner e a condutividade térmica do material é .
Sabemos que
Dessa forma, temos que:
Substituindo pelos valores conhecidos, temos:
Portanto, a taxa de perda de calor da superfície do recipiente é igual ao ganho de calor da água gelada.
Resposta
E as condições de contorno são: e