Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 33

Reconsidere o Prob. 3-31. Usando EES (ou outro programa), investigue o efeito da condutividade térmica sobre a espessura de isolamento necessária. Trace a espessura do isolamento em função da condutividade térmica do isolamento na faixa 0,0 2   W / m ⋅ K a 0,0 8   W / m ⋅ K e discuta os resultados.

Passo 1

Para resolvermos esta questão, vamos utilizar as fórmulas já desenvolvidas lá na questão 3-31. Nesta questão, escrevemos que a resistência térmica de isolamento era expressa por:

R i s o l a m e n t o = L i s o l a m e n t o k i s o l a m e n t o A = Δ T Q ˙ f i n a l - R c o m b

Isolando a variável L i s o l a m e n t o em função de k i s o l a m e n t o , pois todas as outras variáveis são constantes do nosso problema, temos a seguinte função:

L i s o l a m e n t o = Δ T Q ˙ f i n a l - R c o m b ⋅ A ⋅ k i s o l a m e n t o

Substituindo os valores das constantes, temos:

L i s o l a m e n t o = 110 - 32 234 - 0,03333 ⋅ 3 ⋅ k i s o l a m e n t o

L i s o l a m e n t o = 0,9 ⋅ k i s o l a m e n t o

Plotando esta função, temos o seguinte gráfico:

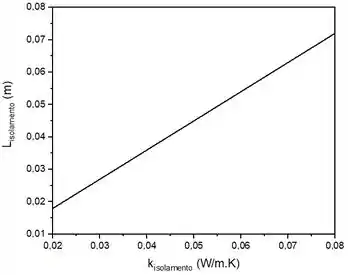
Resultado este esperado. À medida que aumentamos o coeficiente de condução, aumentamos a capacidade do meio de trocar calor. Como queremos reduzir esta capacidade, será necessário aumentar a camada de isolamento, como pode ser observado pelo gráfico.

Resposta

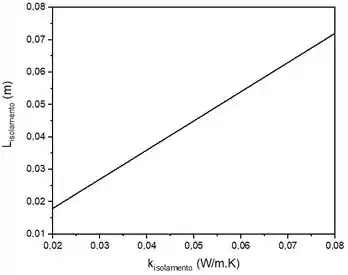
À medida que aumentamos o coeficiente de condução, aumentamos a capacidade do meio de trocar calor. Como queremos reduzir esta capacidade, será necessário aumentar a camada de isolamento.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa específica, o calor específico e a condutividade térmica de um agregado de concreto de baixo peso que é composto por 65 % de concreto (com pedra misturada) e 35 % de ar, em volume. A
Um lote de isolante de fibra de vidro tem a massa específica de ρ = 28k g / m 3 . Determine os valores máximo e mínimo possíveis da condutividade térmica efetiva do isolante a T=300K e compare com os
Uma parede plana unidimensional, com espessura L, é construída com um material sólido com uma distribuição linear e não uniforme de porosidade, descrita por ε ( x )=ε m á x ( x / L á ). Represente gra
Para uma pequena fonte de calor fixada a um grande substrato, a resistência de espalhamento associada à condução multidimensional no substrato pode ser aproximada pela expressão R T ( e s p ) = 1 - 1,
Usando as relações para as resistências térmicas desenvolvidas no Capítulo 3, determine expressões para o fator de forma para as seguintes geometrias: a) Parede plana, casca cilíndrica e casca esféric