Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 82
Reconsidere o Problema 3-80E. Usando o software EES (ou outro programa), investigue os efeitos da condutividade térmica do material do tubo e do diâmetro externo do tubo no comprimento do tubo necessário. Deixe a condutividade térmica variar de a e o diâmetro externo de 1,2 a 2,4 cm. Plote o comprimento do tubo em função da condutividade do e do diâmetro externo do tubo e discuta os resultados.
Passo 1
Legal galerinha, se nós estamos variando somente a resistência do metal a única resistência que irá variar é a resistência do tubo, ok?
E variando a resistência do tubo variamos também a resistência total e o calor por metro do tubo.
A variação total do calor não varia, mas como variamos o calor por metro, nós teremos novos valores para o comprimento.
Usando o Excel podemos obter:
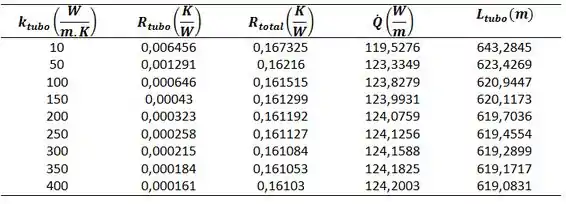
Traçando o gráfico:
Passo 2
Agora, quando variamos o diâmetro externo nós variamos a área externa e, consequentemente a resistência externa e a do tubo.
Agora faremos a mesma coisa:
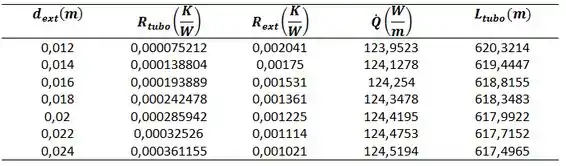
Plotamos gráfico:
Concluímos que, aumentando o diâmetro externo ou a condutividade térmica nós iremos precisar de um comprimento menor do tubo para alcançar a mesma troca de calor!!
E finalizamos esta daqui !!
Resposta
