Uma longa haste cilíndrica de diâmetro de com condutividade térmica de experimenta geração de calor volumétrico uniforme de . A haste é encapsulada por uma luva circular com um diâmetro externo de e uma condutividade térmica de . A superfície externa da luva é exposta ao fluxo cruzado de ar a com um coeficiente de convecção de .

(a) Encontre a temperatura na interface entre a haste e a manga e na superfície externa.

(b) Qual é a temperatura no centro da haste?

Para resolver essa questão, podemos fazer um circuito térmico que representa a condução de calor no sistema. O circuito tem a seguinte forma:

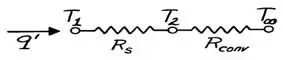
Do circuito térmico, podemos escrever o seguinte:

Nós não temos , podemos encontrar a taxa de transferência de calor por unidade de comprimento usando a seguinte expressão:

(a) Para encontrar a temperatura na interface, podemos usar a seguinte expressão:

Substituindo os termos da expressão acima pelos dados fornecidos, temos:

Portanto, a temperatura na interface é .

Nó fizemos a suposição de estado estacionário, portanto, podemos dizer que:

Logo

Substituindo os termos da expressão acima pelos dados fornecidos, temos:

Portanto, a temperatura na superfície é .

(b) Para resolver essa parte, podemos utilizar a equação para o perfil de temperatura vista nessa seção, só que para o ponto em . A equação é a seguinte:

Para , temos:

Substituindo os termos da expressão acima pelos dados fornecidos, temos:

Portanto, a temperatura no centro da haste é .