Considere duas placas paralelas metálicas muito grandes. A placa superior está a uma temperatura Tsup = 400 K, enquanto a placa inferior está a Tinf = 300 K. O fluxo térmico radiante líquido desejado entre as duas placas é de q″ = 330 W/m².

1. Se as duas superfícies tiverem as mesmas propriedades radiantes, mostre que a emissividade superficial requerida é de ε = 0,5.
2. Superfícies metálicas a temperaturas relativamente baixas tendem a ter emissividades muito menores do que 0,5 (veja Tabela A.11). Um engenheiro propõe usar um padrão de teste, similar ao do Problema 12.132, sobre cada uma das placas metálicas de modo que a metade de cada superfície é caracterizada pela baixa emissividade do metal sem cobertura e a outra metade é coberta pela tinta de alta emissividade. Se a média entre as emissividades alta e baixa for 0,5, o fluxo térmico radiante líquido entre as superfícies terá o valor desejado?

Na letra (b) nós devemos analisar fluxo térmico radiante líquido entre as superfícies terá o valor desejado para um novo caso!!

Aqui nós temos sobre cada uma das placas metálicas de modo que a metade de cada superfície é caracterizada pela baixa emissividade do metal sem cobertura e a outra metade é coberta pela tinta de alta emissividade, neste caso a média entre as emissividades alta e baixa é 0,5, tranquilo ?!

O projeto proposto no Problema 12.132 possui o padrão quadriculado da seguinte forma:

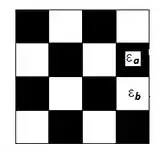
Então vão existir quatro superfícies diferentes: a região de alta emissividade na superfície superior (1a), a região de baixa emissividade na superfície superior (1b), a região de alta emissividade na superfície inferior (2a) e a região de baixa emissividade na superfície inferior (2b).

Bom, já sabemos que o fator forma entre uma região na placa superior e uma região na placa inferior é 0,5, ou seja:

Utilizando o somatório nós concluímos que:

E o que nós fazemos com isso?

Bom, como nós temos quatro regiões envolvidas nesta troca de calor por radiação podemos utilizar as seguintes equações, já substituindo nossos fatores de forma para facilitar:

Chamando:

E manipulando matematicamente as equações acima para achar as radiosidades:

Bom, achamos muita coisa e nada, não foi ? kkkkk

Mas se acalmem !! Vocês vão ver porque tivemos que fazer isso !!

O que nós queremos é o fluxo radiante para este novo caso, certo?

E para isso nós podemos calcular quanto cada quadrado “escuro” e quanto quadrado “branco” do nosso desenho contribuem para o fluxo total:

Nós podemos ver pelo desenho que:

Substituindo:

Para achar e vamos usar o somatório:

Aplicando:

Agora nós vamos substituir as radiosidades que vimos no Passo 2:

E depois de muita manipulação matemática nós chegamos na seguinte expressão:

Igualzinha a expressão do Passo 1, certo?

Então, se nós teremos !!

Concluímos então que ambos os casos possuem o fluxo de calor desejado !!